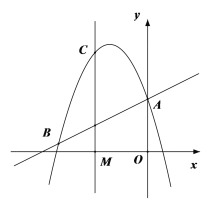Question

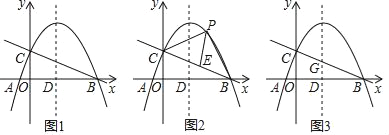
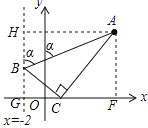
【题目】如图，已知点A（3，4），点B为直线x＝﹣2上的动点，点C（x，0）且﹣2＜x＜3，BC⊥AC垂足为点C，连接AB．若AB与y轴正半轴的所夹锐角为α，当tanα的值最大时x的值为（　　）

A.B.C.1D.

Answer 1

【答案】A

【解析】

设直线x＝2与x轴交于G，过A作AH⊥直线x＝2于H，AF⊥x轴于F，根据平行线的性质得到∠ABH＝α，由三角函数的定义得到tanα＝，即可得当BH最小时tanα有最大值；即BG最大时，tanα有最大值，然后证明△ACF∽△CBG，根据相似三角形的性质列出比例式，最后根据二次函数的性质即可得到结论．

如图，设直线x＝﹣2与x轴交于G，过A作AH⊥直线x＝﹣2于H，AF⊥x轴于F，

∵BH∥y轴，

∴∠ABH＝α，

在Rt△ABH中，tanα＝，

∵tanα随BH的增大而减小，

∴当BH最小时tanα有最大值；即BG最大时，tanα有最大值，

∵∠BGC＝∠ACB＝∠AFC＝90°，

∴∠GBC+∠BCG＝∠BCG+∠ACF＝90°，

∴∠GBC＝∠ACF，

∴△ACF∽△CBG，

∴，

设BG=y，则，

∴，

∴当x＝时，BG取最大值，tanα取最大值，

故选：A．