题目内容
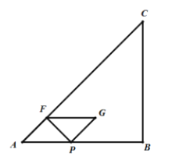
【题目】如图,在等腰直角![]() 中,
中,![]() 动点
动点![]() 以每秒
以每秒![]() 个单位长度的速度从点
个单位长度的速度从点![]() 向终点
向终点![]() 运动,过点
运动,过点![]() 作
作![]() 于点
于点![]() 以
以![]() 为邻边作
为邻边作![]() 与等腰直角
与等腰直角![]() 的重叠部分面积为
的重叠部分面积为![]() (平方单位),
(平方单位),![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出点![]() 落在
落在![]() 边上时的
边上时的![]() 值.
值.
(2)求![]() 与
与![]() 的函数关系式
的函数关系式
(3)直接写出点![]() 分别落在
分别落在![]() 三边的垂直平分线上时的
三边的垂直平分线上时的![]() 值
值
【答案】(1)![]() ;(2)
;(2)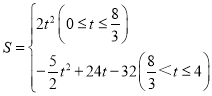 ;(3)
;(3)![]() 或2或4
或2或4
【解析】
(1)画出图形,根据题干条件,得出△AFP和△BPG是等腰直角三角形,表示出AP,PB,根据FQ=BG解出t值;
(2)分当点G在BC边上以及BC左侧时,当点G在BC右侧时,两种情况分别求出S和t的关系即可;
(3)分点G在AB、BC、AC的中垂线上求出t值即可.
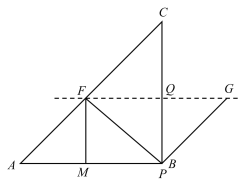
解:(1)当点G落在BC边上时,如图,
∵AB=BC=8,∠B=90°,PF⊥AF,
∴在□APGF中,∠AFP=∠FPG=90°,
∴∠A=∠FPA=∠GPB=∠PGB=45°,
即△AFP和△BPG是等腰直角三角形,
∴AP=FG=2t,PB=BG=8-2t,
AP边上的高FQ=BG=2t,
∴(8-2t)×2=2t,
解得:t=![]() ;
;
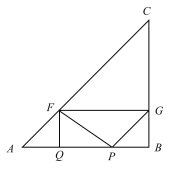
(2)当点G在BC边上以及BC左侧时,0≤t≤![]() ,
,
S的值为□APGF的面积,
△APF为等腰直角三角形,
∴△APF中AP边上的高为t,
则S=2t2,
当点G在BC右侧时,![]() <t≤4,
<t≤4,
由题意可得:∠G=45°,∠NMG=90°,FQ=t,
∴△MNG是等腰直角三角形,
∴MN=MG=MB-NB=MB-PB=t-(8-2t)=3t-8,
S=S□APGF -S△MNG=2t×t-![]() (3t-8)2=
(3t-8)2=![]() ,
,
故S和t的函数关系式为: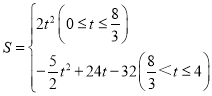 ;
;
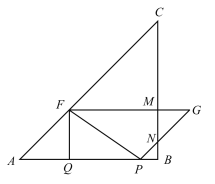
(3)当点G在AB边的中垂线QH上时,
AH=4,
由题意可得:GH=PH=4-2t,
FM=![]() AP=t,
AP=t,
∴4-2t=t,
解得t=![]() ;
;
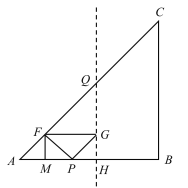
当点G在AC边的中垂线上时,
可知∠ABQ=45°,
∴△PBG为等腰直角三角形,
∴PB=![]() PG=
PG=![]() AF=AP,
AF=AP,
∴AP=4,
∴t=2;
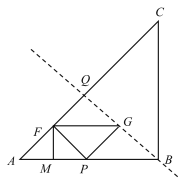
当点G在BC边中垂线上时,
PQ=FM=![]() AP,
AP,
则此时点P与点B重合,
∴t=4.
综上所述:点![]() 分别落在
分别落在![]() 三边的垂直平分线上时,t的值为
三边的垂直平分线上时,t的值为![]() 或2或4.
或2或4.

 名校课堂系列答案
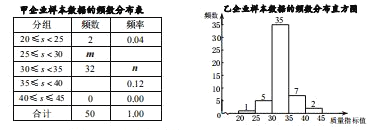
名校课堂系列答案【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了 50 件产品并对某一项关键质量指标做检测,获得了它们的质量指标值 s ,并对样本数据(质量指标值 s )进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 | 20 ≤ s 25 | 25 ≤ s 30 | 30 ≤ s 35 | 35 ≤ s 40 | 40 ≤ s ≤ 45 |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀); 等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整):
c.乙企业样本数据的频数分布直方图如下:
d.两企业样本数据的平均数、中位数、众数、方差如下:
平均数 | 中位数 | 众数 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 15.34 |
根据以上信息,回答下列问题:
(1) m 的值为 , n 的值为 ;
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为 ; 若乙企业生产的某批产品共5 万件,估计质量优秀的有 万件;
(3)根据图表数据,你认为 企业生产的产品质量较好,理由为 .(从某个角度说明推断的合理性)