题目内容
【题目】将矩形![]() 绕点
绕点![]() 顺时针旋转得到矩形
顺时针旋转得到矩形![]() ,点
,点![]() 的对应点分别为
的对应点分别为![]()
(1)当点![]() 落在
落在![]() 上时
上时
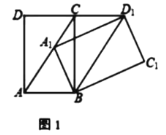
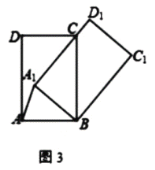
①如图1,若![]() ,求证:
,求证:![]()
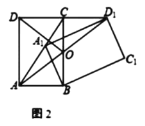
②如图2,![]() 交
交![]() 于点
于点![]() .若
.若![]() ,求证:
,求证:![]() ;
;
(2)若![]() ,
,
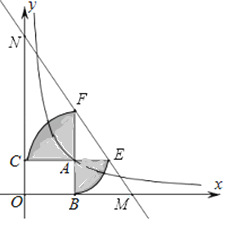
①如图3,当![]() 过点C时,则
过点C时,则![]() 的长=_____.
的长=_____.
②当![]() 时,作
时,作![]() ,
,![]() 绕点
绕点![]() 转动,当直线
转动,当直线![]() 经过
经过![]() 时,直线
时,直线![]() 交边
交边![]() 于
于![]() ,
,![]() 的值=______.
的值=______.
【答案】(1)①见解析,②见解析;(2)①![]() ,②
,②![]()
【解析】
(1)①首先证明△A1B是等边三角形,可得∠AA1B=∠A1BD1=60°,即可解决问题.
②首先证明Rt△BCD1≌RtD1A1B(HL),得到四边形ABD1C是平行四边形,推出OC=OB,再证明△DCO≌△ABO(SAS)即可解决问题.
(2)①如图3中,作A1E⊥AB于E,A1F⊥BC于F.利用勾股定理求出AE,A1E即可解决问题;
②分两种情况,当△A1BE旋转到图4位置时以及当△A1BE旋转到图5位置时,分别证明△DAN∽△BEN即利用相似比得到![]() .
.
(1)证明:①∵∠CAB=60°,
由旋转可知,BA=BA1,
∴△ABA1是等边三角形,
∴∠AA1B=60°,
∵∠A1BD1=∠CAB =60°,
∴∠AA1B=∠A1BD1,![]() ;
;
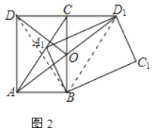
②如图2中,连接BD1,BD,DD1.
由旋转可知:BA=BA1,BD=BD1,∠ABA1=∠DBD1,
∴∠BAA1=∠BDD1,
∵在矩形ABCD中,∠BAA1=∠ABD=∠BDC,
∴∠BDC=∠BDD1,
∴D,C,D1共线,
∵∠BCD1=∠BA1D1=90°,
∴在中Rt△BCD1与RtD1A1B中
BD1=D1B,BC=A1D1,
∴Rt△BCD1≌RtD1A1B(HL),
∴CD1=BA1,
∵BA=BA1,
∴AB=CD1,
∵AC=BD1
∴四边形ABD1C是平行四边形,
∴OC=OB
∵CD=BA,∠DCO=∠ABO=90°,
∴△DCO≌△ABO(SAS),
∴DO=OA.
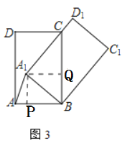
(2)①如图3中,作A1P⊥AB于P,A1Q⊥BC于Q.
在Rt△A1BC中,∵∠CA1B=90°,BC=15.A1B=CD=9,
∴CA1=![]() ,
,
∵![]() ,
,
∴A1Q=![]() ,
,
∵∠A1QB=∠A1PB=∠PBQ=90°,
∴四边形A1PBQ是矩形,
∴PB=A1Q=![]() ,A1P=BQ=
,A1P=BQ=![]() ,
,
∴AP=9![]() =
=![]() ,
,
在Rt△AA1E中,AA1=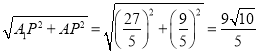 ,
,
故答案为:![]()
②当△A1BE旋转到图4位置时,直线A1E经过点D,
由旋转可知,A1B=AB=9,
∵∠A1BE=45°,∠A1EB=90°,
∴BE=A1E=![]() ,
,
∵∠A1EB=∠DAN=90°,∠AND=∠ENB,
∴△AND∽△ENB,
∴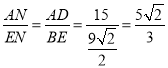 ,
,
当△A1BE旋转到图5位置时,直线A1E经过点D,
由旋转可知,A1B=AB=9,
∵∠A1BE=45°,∠A1EB=90°,
∴BE=A1E=![]() ,
,
∵∠DAN=∠BEN=90°,∠AND=∠ENB,
∴△DAN∽△BEN,
∴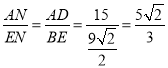 ,
,
综上所述,![]() ,
,
故答案为:![]() .
.

 阅读快车系列答案
阅读快车系列答案