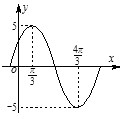
[题目]以直角坐标系的原点O为极点.x轴的正半轴为极轴建立极坐标系.已知点P的直角坐标为(1.2).点M的极坐标为 .若直线l过点P.且倾斜角为 .圆C以M为圆心.3为半径． (Ⅰ)求直线l的参数方程和圆C的极坐标方程,(Ⅱ)设直线l与圆C相交于A.B两点.求|PA||PB|．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】以直角坐标系的原点O为极点，x轴的正半轴为极轴建立极坐标系，已知点P的直角坐标为（1，2），点M的极坐标为，若直线l过点P，且倾斜角为，圆C以M为圆心，3为半径．（Ⅰ）求直线l的参数方程和圆C的极坐标方程；
（Ⅱ）设直线l与圆C相交于A，B两点，求|PA||PB|．

【答案】解：（Ⅰ）直线l的参数方程为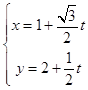（t为参数），圆的极坐标方程为ρ=6sinθ．
（Ⅱ）把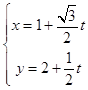代入x2+（y﹣3）2=9，得，
设点A，B对应的参数分别为t1 ， t2 ，
∴t1t2=﹣7，则|PA|=|t1|，|PB|=|t2|，∴|PA||PB|=7
【解析】（I）根据题意直接求直线l的参数方程和圆C的极坐标方程．（II）把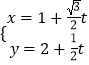代入x2+（y﹣3）2=9，利用参数的几何意义，即可得出结论．

练习册系列答案

相关题目

【题目】宜宾市某化工厂，现有A种原料52千克，B种原料64千克，现用这些原料生产甲、乙两种产品共20件．已知生产1件甲种产品需要A种原料3千克，B种原料2千克；生产1件乙种产品需要A种原料2千克，B种原料4千克，则生产方案的种数为（　　）
A.4
B.5
C.6
D.7

【题目】已知函数．（a为常数，a＞0）（Ⅰ）若是函数f（x）的一个极值点，求a的值；
（Ⅱ）求证：当0＜a≤2时，f（x）在上是增函数；
（Ⅲ）若对任意的a∈（1，2），总存在，使不等式f（x0）＞m（1﹣a2）成立，求实数m的取值范围．

【题目】已知函数f （x）=Asin（ωx+φ），（0＜φ＜π）的图象如图所示，若f（x0）=3，x0∈（，），则sinx0的值为（）
A.
B.
C.
D.

【题目】已知A、B分别在射线CM、CN（不含端点C）上运动，∠MCN= π，在△ABC中，角A、B、C所对的边分别是a、b、c．
（Ⅰ）若a、b、c依次成等差数列，且公差为2．求c的值；
（Ⅱ）若c= ，∠ABC=θ，试用θ表示△ABC的周长，并求周长的最大值．

【题目】已知椭圆内有一点M（2，1），过M的两条直线l1 ， l2分别与椭圆E交于A，C和B，D两点，且满足（其中λ＞0，且λ≠1），若λ变化时，AB的斜率总为，则椭圆E的离心率为（）
A.
B.
C.
D.

【题目】据某市地产数据研究院的数据显示，2016年该市新建住宅销售均价走势如图所示，为抑制房价过快上涨，政府从8月份采取宏观调控措施，10月份开始房价得到很好的抑制．
（Ⅰ）地产数据研究院研究发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试建立y关于x的回归方程（系数精确到0.01），政府若不调控，依次相关关系预测第12月份该市新建住宅销售均价；
（Ⅱ）地产数据研究院在2016年的12个月份中，随机抽取三个月份的数据作样本分析，若关注所抽三个月份的所属季度，记不同季度的个数为X，求X的分布列和数学期望．
参考数据： =25， =5.36， =0.64
回归方程 = x+ 中斜率和截距的最小二乘估计公式分别为：
= ， = ﹣ ．

【题目】已知函数f（x）= （e为自然对数的底数），曲线y=f（x）在（1，f（1））处的切线与直线4x+3ey+1=0互相垂直．（Ⅰ）求实数a的值；
（Ⅱ）若对任意x∈（，+∞），（x+1）f（x）≥m（2x﹣1）恒成立，求实数m的取值范围；
（Ⅲ）设g（x）= ，Tn=1+2[g（）+g（）+g（）+…+g（）]（n=2，3…）．问：是否存在正常数M，对任意给定的正整数n（n≥2），都有 + + +…+ ＜M成立？若存在，求M的最小值；若不存在，请说明理由．

【题目】某地区住宅用电之电费计算规则如下：每月每户不超过50度时，每度以4元收费；超过50度的部分，每度以5元收费，并规定用电按整数度计算(小数部份无条件舍去) ．
（1）下表给出了今年3月份A，B两用户的部分用电数据，请将表格数据补充完整，

	电量（度）	电费（元）
A		240
B
合计	90

（2）若假定某月份C用户比D用户多缴电费38元，求C用户该月可能缴的电费为多少？

试题分类