题目内容
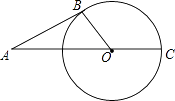
【题目】如图,△ACB和△DCE均为等腰三角形,点A、D、E在同一条直线上,BC和AE相交于点O,连接BE,若∠CAB=∠CBA=∠CDE=∠CED=50°。
(1)求证:AD=BE;
(2)求∠AEB。
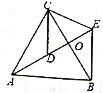
【答案】(1)详见解析;(2)∠AEB=80°.
【解析】
(1)欲证明AD=BE,只要证明△ACD≌△BCE(SAS)即可.
(2)利用:“8字型”可以证明∠OEB=∠ACO,即可解决问题.
(1)证明:
∵∠CAB=∠CBA=∠CDE=∠CED=50°,
∴CA=CB,CD=CE,∠ACB=∠DCE=80°,∴∠ACD=∠BCE,
在△ACD和△BCE中,
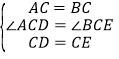 ,∴△ACD≌△BCE(SAS),
,∴△ACD≌△BCE(SAS),
∴AD=BE.
(2)解:∵△ACD≌△BCE,∴∠CAD=∠CBE,
∵∠COA=∠BOE,∴∠ACO=∠BEO=80°,
∴∠AEB=80°.

练习册系列答案
相关题目