题目内容
【题目】如图，一次函数y=kx+b的图象与反比例函数y= 
的图象交于点A（﹣2，﹣5 ），C （5，n），交y轴于点B，交x轴于点D，那么不等式kx+b﹣ ＞0的解集是 ．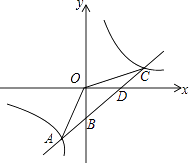 
【答案】﹣2＜x＜0或x＞5
【解析】解：∵反比例函数y= 
的图象经过点A（﹣2，﹣5 ）， ∴m=（﹣2）×（﹣5）=10，
∴反比例函数的表达式为y= 
，
∵点C （5，n）在反比例函数的图象上，
∴n= 
=2，
∴C的坐标为C（5，2），
∵一次函数的图象经过点A，C，将这两个点的坐标代入y=kx+b，得
，
解得 
，
∴一次函数的表达式为y=x﹣3，
根据图象法可得，当一次函数的图象在反比例函数的图象上边时，对应的自变量x的范围是：﹣2＜x＜0或x＞5，
∴不等式x﹣3﹣ ＞0的解集是：﹣2＜x＜0或x＞5．
所以答案是：﹣2＜x＜0或x＞5．
【考点精析】关于本题考查的确定一次函数的表达式，需要了解确定一个一次函数，需要确定一次函数定义式y=kx+b（k不等于0）中的常数k和b．解这类问题的一般方法是待定系数法才能得出正确答案．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：
组号 | 分组 | 频数 |
一 | 6≤m＜7 | 2 |
二 | 7≤m＜8 | 7 |
三 | 8≤m＜9 | a |
四 | 9≤m≤10 | 2 |
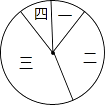
（1）求a的值；
（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；
（3）将在第一组内的两名选手记为：A1、A2 ， 在第四组内的两名选手记为：B1、B2 ， 从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．
