题目内容
【题目】如图,直线AB∥CD,EF分别交AB、CD于G、F两点,射线FM平分∠EFD,将射线FM平移,使得端点F与点G重合且得到射线GN.若∠EFC=110°,则∠AGN的度数是( )
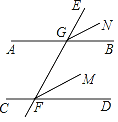
A. 120° B. 125° C. 135° D. 145°
【答案】D
【解析】
先根据邻补角的定义可求得∠EFD=70°,再根据角平分线的定义求得∠EFM=35°,由平移的性质可得GN//FM,继而可得∠EGN=∠EFM=35°,再根据AB//CD,可得∠AGE=∠EFC=110°,再由∠AGN=∠AGE+∠EGN即可得解.
∵∠EFC=110°,∠EFC+∠EFD=180°,
∴∠EFD=70°,
∵FM平分∠EFD,
∴∠EFM=35°,
∵将射线FM平移,使得端点F与点G重合且得到射线GN,
∴GN//FM,
∴∠EGN=∠EFM=35°,
∵AB//CD,
∴∠AGE=∠EFC=110°,
∴∠AGN=∠AGE+∠EGN=110°+35°=145°,
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目