题目内容
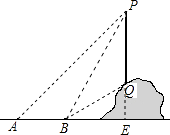
【题目】如图，从地面上的点A看一山坡上的电线杆PQ，测得杆顶端点P的仰角是45°，向前走6m到达B点，测得杆顶端点P和杆底端点Q的仰角分别是60°和30°．
（1）求∠BPQ的度数；
（2）求该电线杆PQ的高度（结果精确到1m）．
备用数据： 
， 
．
【答案】
（1）
解：解：延长PQ交直线AB于点E，
∠BPQ=90°﹣60°=30°
（2）
解：设PE=x米．
在直角△APE中，∠A=45°，
则AE=PE=x米；
∵∠PBE=60°
∴∠BPE=30°
在直角△BPE中，BE= 
PE= x米，
∵AB=AE﹣BE=6米，
则x﹣ x=6，
解得：x=9+3 
．
则BE=（3 +3）米．
在直角△BEQ中，QE= BE= （3 +3）=（3+ ）米．
∴PQ=PE﹣QE=9+3 ﹣（3+ ）=6+2 ≈9（米）．
答：电线杆PQ的高度约9米
【解析】（1）延长PQ交直线AB于点E，根据直角三角形两锐角互余求得即可；（2）设PE=x米，在直角△APE和直角△BPE中，根据三角函数利用x表示出AE和BE，根据AB=AE﹣BE即可列出方程求得x的值，再在直角△BQE中利用三角函数求得QE的长，则PQ的长度即可求解．
【考点精析】关于本题考查的关于仰角俯角问题，需要了解仰角：视线在水平线上方的角；俯角：视线在水平线下方的角才能得出正确答案．
练习册系列答案
相关题目
