题目内容
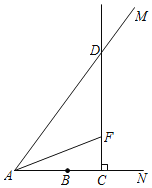
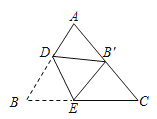
【题目】如图,在△ABC中,AB=AC=5,BC=6,点D,E分别在AB,BC上,将△ABC沿直线DE折叠,点B落在AC的中点B′处,则BE的长为_____.
【答案】![]()
【解析】
如图,过点A作AH⊥BC,取CH中点F,连接B'F,由等腰三角形的性质和勾股定理可求AH=4,BH=CH=3,由三角形中位线定理可求B'F=![]() AH=2,CF=
AH=2,CF=![]() CH=
CH=![]() ,B'F∥AH,由勾股定理可求BE的长.
,B'F∥AH,由勾股定理可求BE的长.
解:如图,过点A作AH⊥BC,取CH中点F,连接B'F,
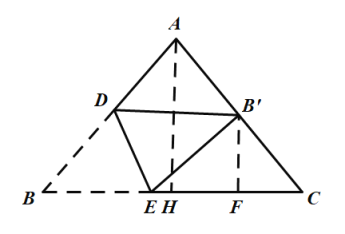
∵AB=AC=5,BC=6,AH⊥BC,
∴BH=HC=3,
∴AH=![]() ,
,
∵点B'是AC中点,点F是CH中点,
∴B'F=![]() AH=2,CF=
AH=2,CF=![]() CH=
CH=![]() ,B'F∥AH,
,B'F∥AH,
∴∠AHC=∠B'FC=90°,
∴BF=BC﹣CF=![]() ,
,
∵将△ABC沿直线DE折叠,点B落在AC的中点B′处,
∴BE=B'E,
∵B'E2=B'F2+EF2,
∴BE2=4+(![]() ﹣BE)2,
﹣BE)2,
∴BE=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目