题目内容
【题目】（1）观察下列图形与等式的关系，并填空：
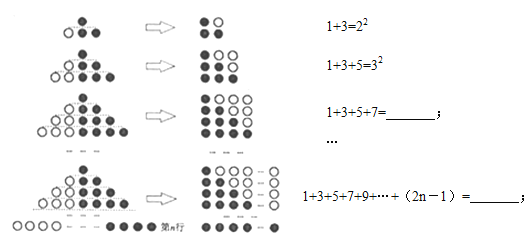
（2）利用（1）中结论，解决下列问题：
①1+3+5+…+2005= ；
②计算：101+103+105+…+199；
【答案】（1）16，
；（2）①
；②7500.
【解析】
（1）根据题目中的式子特点，即可得出答案；
（2）①根据（1）中的结论即可得出答案；②对所求式子进行变形即可得出答案.
（1）∵1+3=
1+3+5=
1+3+5+7=
……
∴1+3+5+…+（2n-1）=
（2）①由（1）可得：1+3+5+…+2005=1+3+5+…+(2×1003-1)=
②∵1+3+5+…+99=1+3+5+…+（2×50-1）=
1+3+5+…+199=1+3+5+…+（2×100-1）=
∴101+103+…+109=（1+3+5+…+199）-（1+3+5+…+99）=
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
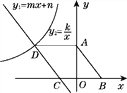
【题目】已知二次函数
．
（
）将
化成
的形式．
（
）与
轴的交点坐标是__________，与
轴的交点坐标是__________．
（
）在坐标系中利用描点法画出此抛物线．
|
|
| |||||
|
|
|
