题目内容
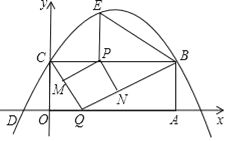
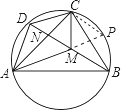
【题目】如图,已知圆内接四边形ABCD的对角线AC、BD交于点N,点M在对角线BD上,且满足∠BAM=∠DAN,∠BCM=∠DCN.
求证:(1)M为BD的中点;(2)![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)要证M为BD的中点,即证BM=DM,由∠BAM=∠DAN,∠BCM=∠DCN,及圆周角的性质易证明△BAM∽△CBM,△DAM∽△CDM得出比例的乘积形式,可证明BM=DM;
(2)欲证![]() ,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
,可以通过平行线的性质证明,需要延长AM交圆于点P,连接CP,证明PC∥BD,得出比例式,相应解决MP=CM的问题即可.
试题解析:(1)根据同弧所对的圆周角相等,得∠DAN=∠DBC,∠DCN=∠DBA,
又∵∠DAN=∠BAM,∠BCM=∠DCN,
∴∠BAM=∠MBC,∠ABM=∠BCM,
∴△BAM∽△CBM,
∴![]() ,即BM2=AMCM ,①
,即BM2=AMCM ,①
又∠DCM=∠DCN+∠NCM=∠BCM+∠NCM=∠ACB=∠ADB,
∠DAM=∠MAC+∠DAN=∠MAC+∠BAM=∠BAC=∠CDM,
∴△DAM∽△CDM,
则![]() ,即DM2=AMCM ,②
,即DM2=AMCM ,②
由式①、②得:BM=DM,
即M为BD的中点;
(2)如图,延长AM交圆于点P,连接CP,
∴∠BCP=∠PAB=∠DAC=∠DBC,
∵PC∥BD,
∴![]() , ③
, ③
又∵∠MCB=∠DCA=∠ABD,∠DBC=∠PCB,
∴∠ABC=∠MCP,
而∠ABC=∠APC,
则∠APC=∠MCP,
有MP=CM,④
由式③、④得: ![]() .
.

练习册系列答案
相关题目