��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪OΪԭ�㣬�ı���ABCDΪƽ���ı��Σ�A��B��C������ֱ���A����5��1����B����2��4����C��5��4������D�ڵ�һ���ޣ� 
��1��д��D������ꣻ
��2����B��D�����ֱ�ߵĽ���ʽ�������߶�BD�ij���
��3����ƽ���ı���ABCD������ƽ��1����λ���ȣ�������ƽ��1����λ�������õ��ı���A1B1C1D1�ĸ�����������Ƕ��٣������ƽ���ı���ABCD���ı���A1B1C1D1�ص����ֵ������
���𰸡�
��1���⣺��B����2��4����C��5��4����
��BC=5������2��=5+2=7��
��A����5��1����
���D�ĺ�����Ϊ��5+7=2��
���D��������2��1����
��2���⣺��ֱ��BD�Ľ���ʽΪy=kx+b��
��B����2��4����D��2��1������ã� ![]() ��
��
��� 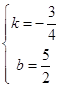 ��
��
�ྭ��B��D�����ֱ�ߵĽ���ʽΪy=�� ![]() x+
x+ ![]() ��
��
��B����AD�Ĵ��ߣ�����ΪE����BE=4��1=3��

DE=2������2��=2+2=4��
��Rt��BDE��BD= ![]() =
= ![]() =5��
=5��
��3���⣺��ABCD����ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ�
��A1����4��0����B1����1��3����C1��6��3��D1��3��0����
���ص����ֵĵױ߳�7��1��1=5��
��Ϊ3��1=2��
���ص����ֵ����S=5��2=10��
����������1�����ݵ�B��C���������BC�ij��ȣ��ٸ���ƽ���ı��εĶԱ������ʽ�����D�ĺ����꣬Ȼ��д��D�����꼴�ɣ���2����ֱ��BD�Ľ���ʽΪy=kx+b��Ȼ�����ô���ϵ������һ�κ�������ʽ��𣻹���B��BE��AD��E�����BE��DE�ij���Ȼ�����ù��ɶ�����ʽ���㼴�ɵý⣻��3����������ƽ�ƺ�����ӣ�����ƽ������������A1��B1��C1��D1�����꣬Ȼ������ص�����ƽ���ı��εĵױߺߣ��ٸ���ƽ���ı��ε������ʽ��ʽ���㼴�ɵý⣮


