题目内容
计算
(1)(-5a2b3)(2a2b);
(2)x3y4÷xy;
(3)
a2bc3•(-2a2b2c)2;
(4)(b-3)(b+3);
(5)(2a+3b)2;
(6)(x+2)2-(x-2)2;
(7)20052(用公式计算);
(8)1999×2001(用公式计算).
(1)(-5a2b3)(2a2b);
(2)x3y4÷xy;
(3)
| 1 |
| 2 |
(4)(b-3)(b+3);
(5)(2a+3b)2;
(6)(x+2)2-(x-2)2;
(7)20052(用公式计算);
(8)1999×2001(用公式计算).
考点:整式的混合运算
专题:计算题
分析:(1)原式利用单项式乘以单项式法则计算即可得到结果;
(2)原式利用单项式除以单项式法则计算即可得到结果;
(3)原式先计算乘方运算,再计算乘法运算即可得到结果;
(4)原式利用平方差公式化简即可得到结果;
(5)原式利用完全平方公式展开即可得到结果;
(6)原式利用完全平方公式展开,去括号合并即可得到结果;
(7)原式变形后,利用完全平方公式展开即可得到结果;
(8)原式变形后,利用平方差公式化简即可得到结果.
(2)原式利用单项式除以单项式法则计算即可得到结果;
(3)原式先计算乘方运算,再计算乘法运算即可得到结果;
(4)原式利用平方差公式化简即可得到结果;
(5)原式利用完全平方公式展开即可得到结果;
(6)原式利用完全平方公式展开,去括号合并即可得到结果;
(7)原式变形后,利用完全平方公式展开即可得到结果;
(8)原式变形后,利用平方差公式化简即可得到结果.
解答:解:(1)(-5a2b3)(2a2b)=-10a4b4;
(2)x3y4÷xy=x2y3;
(3)
a2bc3•(-2a2b2c)2=
a2bc3•4a4b4c=2a6bc5;
(4)(b-3)(b+3)=b2-9;
(5)(2a+3b)2=4a2+12ab+9b2;
(6)(x+2)2-(x-2)2=x2+4x+4-(x2-4x+4)=x2+4x+4-x2+4x-4=8x;
(7)20052=(2000+5)2=20002+2×2000×5+52=4000000+20000+25=4020025;
(8)1999×2001=(2000-1)(2000+1)=20002-12=4000000-1=3999999.
(2)x3y4÷xy=x2y3;
(3)
| 1 |
| 2 |
| 1 |
| 2 |
(4)(b-3)(b+3)=b2-9;
(5)(2a+3b)2=4a2+12ab+9b2;
(6)(x+2)2-(x-2)2=x2+4x+4-(x2-4x+4)=x2+4x+4-x2+4x-4=8x;
(7)20052=(2000+5)2=20002+2×2000×5+52=4000000+20000+25=4020025;
(8)1999×2001=(2000-1)(2000+1)=20002-12=4000000-1=3999999.
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
如果(a+9)x<a+9的解集为x>1,则a需要满足( )
| A、a<0 | B、a≤-9 |
| C、a<9 | D、a<-9 |
 如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由.
如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由.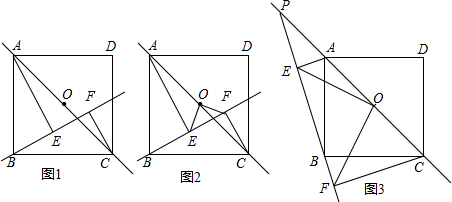
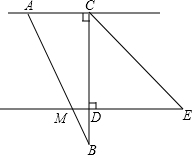 将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.
将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想. 如图,AB是⊙O的直径,C,D是⊙O上两点,且AB=4cm,AC=CD=1cm,求BD的长.
如图,AB是⊙O的直径,C,D是⊙O上两点,且AB=4cm,AC=CD=1cm,求BD的长.