题目内容
用配方法证明：代数式-x2+6x-10恒小于零．
考点：配方法的应用
专题：计算题,配方法
分析：先利用配方法得到-x2+6x-10=-（x-3）2-1，然后根据非负数的性质进行证明．
解答：证明：-x2+6x-10=-（x2-6x）-10
=-（x2-6x+9-9）-10
=-（x-3）2+9-10
=-（x-3）2-1，
∵（x-3）2≥0，
∴-（x-3）2≤0，
∴-（x-3）2-1≤-1，
即代数式-x2+6x-10恒小于零．
=-（x2-6x+9-9）-10
=-（x-3）2+9-10
=-（x-3）2-1，
∵（x-3）2≥0，
∴-（x-3）2≤0，
∴-（x-3）2-1≤-1，
即代数式-x2+6x-10恒小于零．
点评：本题考查了配方法：配方法的理论依据是公式a2±2ab+b2=（a±b）2．也考查了非负数的性质．
练习册系列答案
阅读快车系列答案
相关题目
平行四边形一边长是9cm，这个平行四边形的两条对角线可以是（ ）
| A、11cm和6cm |
| B、6cm和8cm |
| C、8cm和10cm |
| D、10cm和12cm |
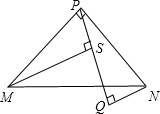如图，在△MPN中，MP=NP，∠MPN=90°，NQ⊥PQ，MS⊥PQ，垂足分别为Q、S．
已知，如图△ABC中，AB=AC，∠A=90°，∠ACB的平分线CD交AB于点E，∠BDC=90°，求证：CE=2BD．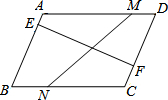
如图，四边形ABCD为平行四边形，M、N分别从D到A、从B到C，速度相同，E、F分别从A到B、从C到D，速度相同．他们之间用绳子连紧．