题目内容
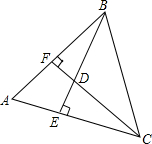 如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由.
如图,已知AB=AC,CF⊥AB于F,BE⊥AC于E,CF与BE交于点D,由这些条件写出所有相等的线段,并说明理由.考点:全等三角形的判定与性质,等腰三角形的性质
专题:几何图形问题
分析:证△ABE≌△ACF,根据全等三角形的性质得出∠ABE=∠ACF,CF=BE,AE=AF,即可求出各个答案.
解答:解:AF=AE,CF=BE,BF=CE,BD=CD,DF=DE,
理由是:∵CF⊥AB,BE⊥AC,
∴∠BEA=∠BEC=∠CFA=∠CFB=90°,
∴在△ABE和△ACF中
∴△ABE≌△ACF,
∴∠ABE=∠ACF,CF=BE,AE=AF,
∵AB=AC,
∴CE=BF,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABE=∠ACF,
∴∠DBC=∠DCB,
∴BD=CD,
∵BE=CF,
∴DF=ED.
理由是:∵CF⊥AB,BE⊥AC,
∴∠BEA=∠BEC=∠CFA=∠CFB=90°,
∴在△ABE和△ACF中
|
∴△ABE≌△ACF,
∴∠ABE=∠ACF,CF=BE,AE=AF,
∵AB=AC,
∴CE=BF,
∵AB=AC,
∴∠ABC=∠ACB,
∵∠ABE=∠ACF,
∴∠DBC=∠DCB,
∴BD=CD,
∵BE=CF,
∴DF=ED.
点评:本题考查了全等三角形的性质和判定的应用,主要考查学生的推理能力,题目比较好,难度适中.

练习册系列答案
相关题目
下列各方程组中,属于二元一次方程组的是( )
A、
| |||||||||||
B、
| |||||||||||
C、
| |||||||||||
D、
|
平行四边形一边长是9cm,这个平行四边形的两条对角线可以是( )
| A、11cm和6cm |
| B、6cm和8cm |
| C、8cm和10cm |
| D、10cm和12cm |
绝对值不大于3.1的整数有( )
| A、4个 | B、5个 | C、6个 | D、7个 |
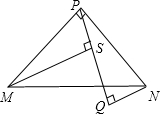 如图,在△MPN中,MP=NP,∠MPN=90°,NQ⊥PQ,MS⊥PQ,垂足分别为Q、S.
如图,在△MPN中,MP=NP,∠MPN=90°,NQ⊥PQ,MS⊥PQ,垂足分别为Q、S.