题目内容
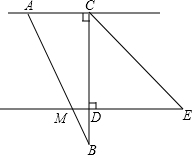 将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.
将一副直角三角板按图所示方式放置,∠ACB=∠CDE=90°,∠CAB=60°,∠ECD=45°,AB边交直线DE于点M,设∠BMD=α,∠BCE=β,将直角三角板ABC绕着点C旋转,在旋转过程中,点B始终位于直线DE下方,猜想变化过程中α与β的数量关系,并利用相交线与平行线的相关知识证明你的猜想.考点:平行线的判定与性质
专题:几何图形问题
分析:分类讨论:当将直角三角板ABC绕着点C逆时针旋转时,根据三角形内角和定理得到α+30°=β+45°,
即α-β=15°;当将直角三角板ABC绕着点C顺时针旋转时,先根据三角形外角性质得∠BMD=∠1+∠B,再根据对顶角性质和三角形内角和定理得∠1=∠2,∠2=180°-∠DEC-∠BCE,所以∠BMD=180°-∠DEC-∠BCE+∠B,即α=180°-45°-β+30°,于是得到α+β=165°.
即α-β=15°;当将直角三角板ABC绕着点C顺时针旋转时,先根据三角形外角性质得∠BMD=∠1+∠B,再根据对顶角性质和三角形内角和定理得∠1=∠2,∠2=180°-∠DEC-∠BCE,所以∠BMD=180°-∠DEC-∠BCE+∠B,即α=180°-45°-β+30°,于是得到α+β=165°.
解答: 解:α与β的数量关系为α-β=15°或α+β=165°.
解:α与β的数量关系为α-β=15°或α+β=165°.
当将直角三角板ABC绕着点C逆时针旋转时,如图1,
∵∠BMD+∠B=∠BDE+∠DEC,
∴α+30°=β+45°,
∴α-β=15°;
当将直角三角板ABC绕着点C顺时针旋转时,如图2,
∵∠BMD=∠1+∠B,
而∠1=∠2,∠2=180°-∠DEC-∠BCE,
∴∠BMD=180°-∠DEC-∠BCE+∠B,
∴α=180°-45°-β+30°,
∴α+β=165°.
 解:α与β的数量关系为α-β=15°或α+β=165°.
解:α与β的数量关系为α-β=15°或α+β=165°.当将直角三角板ABC绕着点C逆时针旋转时,如图1,
∵∠BMD+∠B=∠BDE+∠DEC,
∴α+30°=β+45°,
∴α-β=15°;
当将直角三角板ABC绕着点C顺时针旋转时,如图2,
∵∠BMD=∠1+∠B,
而∠1=∠2,∠2=180°-∠DEC-∠BCE,
∴∠BMD=180°-∠DEC-∠BCE+∠B,
∴α=180°-45°-β+30°,
∴α+β=165°.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行;同旁内角互补,两直线平行;两直线平行,内错角相等;两直线平行,同旁内角互补.也考查了三角形内角和定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
绝对值不大于3.1的整数有( )
| A、4个 | B、5个 | C、6个 | D、7个 |
 已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.
已知,如图△ABC中,AB=AC,∠A=90°,∠ACB的平分线CD交AB于点E,∠BDC=90°,求证:CE=2BD.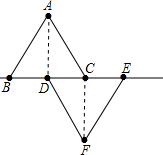 在直角坐标中,有两个边长都为10cm的等边三角形△ABC和△DEF,且BC、DE与x轴重合,B与原点O重合,连结AD、CF.
在直角坐标中,有两个边长都为10cm的等边三角形△ABC和△DEF,且BC、DE与x轴重合,B与原点O重合,连结AD、CF.