��Ŀ����
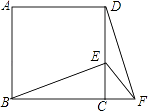
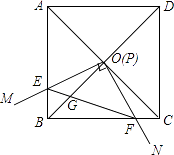
����Ŀ����ͼ���߳�Ϊ1��������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O����ֱ�ǡ�MPN��ʹֱ�Ƕ���P���O�غϣ�ֱ�DZ�PM��PN�ֱ���OA��OB�غϣ�Ȼ����ʱ����ת��MPN����ת��Ϊ�ȣ�0�㣼�ȣ�90�㣩��PM��PN�ֱ�AB��BC��E��F���㣬����EF��OB�ڵ�G�������н�������ȷ���� ��
��1��EF= ![]() OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF=
OE����2��S�ı���OEBF��S������ABCD=1��4����3��BE+BF= ![]() OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE=
OA����4������ת�����У�����BEF���COF�����֮�����ʱ��AE= ![]() ��
��
���𰸡���1����2����3��
���������⣺��1�����ı���ABCD�������Σ�
��OB=OC����OBE=��OCF=45�㣬��BOC=90�㣬
���BOF+��COF=90�㣬
�ߡ�EOF=90�㣬
���BOF+��COE=90�㣬
���BOE=��COF��
�ڡ�BOE�͡�COF�У�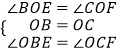 ��
��
���BOE�ա�COF��ASA����
��OE=OF��BE=CF��
��EF= ![]() OE������ȷ��
OE������ȷ��
��2����S�ı���OEBF=S��BOE+S��BOE=S��BOE+S��COF=S��BOC= ![]() S������ABCD ��
S������ABCD ��
��S�ı���OEBF��S������ABCD=1��4������ȷ��
��3����BE+BF=BF+CF=BC= ![]() OA������ȷ��
OA������ȷ��
��4������O��OH��BC��
��BC=1��
��OH= ![]() BC=
BC= ![]() ��
��
��AE=x����BE=CF=1��x��BF=x��
��S��BEF+S��COF= ![]() BEBF+
BEBF+ ![]() CFOH=
CFOH= ![]() x��1��x��+
x��1��x��+ ![]() ��1��x����
��1��x���� ![]() =��
=�� ![]() ��x��
��x�� ![]() ��2+
��2+ ![]() ��
��
��a=�� ![]() ��0��
��0��
�൱x= ![]() ʱ��S��BEF+S��COF���
ʱ��S��BEF+S��COF���
������ת�����У�����BEF���COF�����֮�����ʱ��AE= ![]() ���ʴ���
���ʴ���
�ʴ�Ϊ��1����2����3����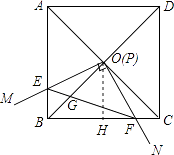
��1�����ı���ABCD�������Σ�ֱ�ǡ�MPN����֤�á�BOE�ա�COF��ASA�������֤�ý��ۣ���2���ɣ�1����֤��S�ı���OEBF=S��BOC= ![]() S������ABCD �� ���֤�ý��ۣ���3����BE=CF���ɵ�BE+BF=BC��Ȼ���ɵ���ֱ�������ε����ʣ�֤��BE+BF=
S������ABCD �� ���֤�ý��ۣ���3����BE=CF���ɵ�BE+BF=BC��Ȼ���ɵ���ֱ�������ε����ʣ�֤��BE+BF= ![]() OA����4��������AE=x����BE=CF=1��x��BF=x���̶���ʾ����BEF���COF�����֮�ͣ�Ȼ�����ö��κ�������ֵ���⣬��ô𰸣�
OA����4��������AE=x����BE=CF=1��x��BF=x���̶���ʾ����BEF���COF�����֮�ͣ�Ȼ�����ö��κ�������ֵ���⣬��ô𰸣�

 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�