题目内容
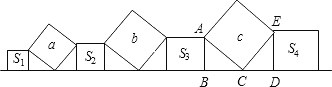
【题目】在直线 l 上依次摆放着七个正方形(如图所示),已知斜放置的三个正方形的面积分别 为 a,b,c,正放置的四个正方形的面积依次为 S1,S2,S3,S4,则 S1+S2+S3+S4=( )
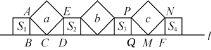
A. a+b B. b+c C. a+c D. a+b+c
【答案】C
【解析】
求证△ABC≌△CDE,得DE=BC,△ABC中AB2+CE2=AC2,根据S3=AB2,S4=DE2可求得S3+S4=c,同理可得S1+S2=a,故S3+S4+S1+S2=a+c.
解:
∵∠ACB+∠DCE=90°,∠BAC+∠ACB=90°,
∴∠DCE=∠BAC,
∵AC=CE,∠ABC=∠CDE,
∴△ABC≌△CDE,
∴BC=DE,
在直角△ABC中,AB2+BC2=AC2,
即,AB2+DE2=AC2,
∵S3=AB2,S4=DE2,
∴S3+S4=c,
同理S1+S2=a,
故可得S1+S2+S3+S4=a+c,
故选:C.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目