题目内容
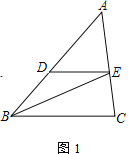
【题目】△ABC中,D、E分别为AB、AC边上的点,DE∥BC,连接BE
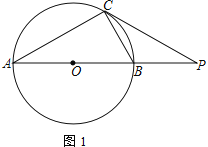
(1)如图1,已知AB=6,AC=5,BC=4.若∠DBE=∠EBC,求DE的长
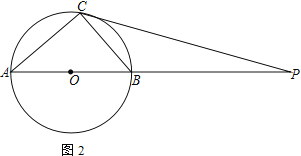
(2)如图2,F为BC的中点,连接DF交BE于G,连接AG交BC于H,求![]() 的值
的值

【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)已知DE∥BC,根据平行线的性质可得∠DEB=∠EBC,△ADE∽△ABC,又因∠DBE=∠EBC,可得∠DBE=∠DEB,所以BD=DE,由△ADE∽△ABC可得![]() ,即
,即![]() ,解得DE=2.4;(2)由DE∥BC可得
,解得DE=2.4;(2)由DE∥BC可得![]() ,即可得
,即可得![]() ,所以BH2=HF·HC,设BF=CF=1,BH=m,则HF=1-m,HC=2-m,根据BH2=HF·HC列出方程m2=(1-m)(1-2m),解得m的值,即可得
,所以BH2=HF·HC,设BF=CF=1,BH=m,则HF=1-m,HC=2-m,根据BH2=HF·HC列出方程m2=(1-m)(1-2m),解得m的值,即可得![]() 的值.
的值.
试题解析:
(1) ![]()
(2)∵DE∥BC
∴![]()
∴![]()
∴BH2=HF·HC
设BF=CF=1,BH=m,则HF=1-m,HC=2-m
∴m2=(1-m)(1-2m),解得m=![]()
∴![]()

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目