题目内容
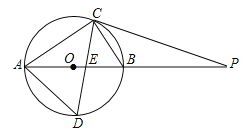
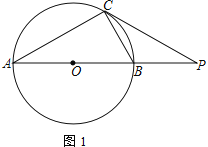
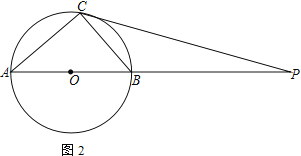
【题目】如图,⊙O为Rt△ACB的外接圆,点P是AB延长线上的一点,PC切⊙O于点C,连AC
(1)若AC=CP,求![]() 的值
的值
(2)若sin∠APC=![]() ,求tan∠ABC
,求tan∠ABC
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析:(1)连接OC,根据已知条件易证△ACO≌△PCB(AAS),根据全等三角形的性质可得OC=BC=OB,可判定△OBC为等边三角形,即求得结论;(2)连接OC,先证△PCB∽△PAC,根据相似三角形的性质可得![]() ,再求得PC的长,即可求得结论.
,再求得PC的长,即可求得结论.
试题解析:
(1)∵AC=CP
∴∠A=∠P
连接OC
∵PC切⊙O于点C
∴∠OCP=90°
∵∠ACB=90°
∴∠ACO=∠PCB
在△ACO和△PCB中

∴△ACO≌△PCB(AAS)
∴OC=BC=OB
∴△OBC为等边三角形
∴∠OBC=60°,∠A=∠P=30°
∴![]()
(2) 连接OC,
∵PC切于点C
∴∠OCP=90°
∴∠PCB+∠OCB=90°
∵∠ACB=90°
∴∠CAB+∠CBA=90°
∵OB=OC
∴∠OBC=∠OCB
∴∠PCB=∠PAC
∴△PCB∽△PAC
∴![]()
∵sin∠APC=![]()
∴设OC=7,OP=25,则OB=OA=7,BP=18
∴![]()
∴PC=12
∴tan∠ABC=![]()


练习册系列答案
相关题目