Question

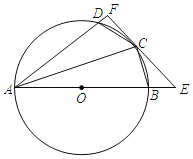
【题目】如图，四边形ABCD内接于⊙O，点O在AB上，BC＝CD，过点C作⊙O的切线，分别交AB，AD的延长线于点E，F．

（1）求证：AF⊥EF；

（2）若cos∠DAB＝，BE＝1，则线段AD的长是_____．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

（1）如图（见解析），连接OC，先根据圆周角定理得出∠1＝∠2，再根据等腰三角形的性质得出∠2＝∠OCA，从而可得∠1＝∠OCA，然后根据平行线的判定可得OC∥AF，最后根据圆的切线的性质得OC⊥EF，从而得到AF⊥EF；

（2）先利用OC∥AF得到∠COE＝∠DAB，在中，设OC＝r，利用余弦的定义得到＝，解得r＝3，如图（见解析），连接BD，根据圆周角定理得到，然后根据余弦的定义即可计算出AD的长．

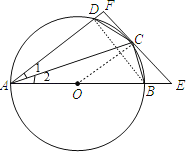
（1）如图，连接OC

∵CD＝BC

∴＝

∴∠1＝∠2

∵OA＝OC

∴∠2＝∠OCA

∴∠1＝∠OCA

∴OC∥AF

∵EF为切线

∴OC⊥EF

∴AF⊥EF；

（2）∵OC∥AF

∴∠COE＝∠DAB

设OC＝r

在中，，即＝

解得r＝3

如图，连接BD

∵AB为直径

∴

在中，，即

解得

故答案为：．