题目内容
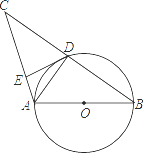
【题目】如图,点P在⊙O的直径BA延长线上,PC与⊙O相切,切点为C,点D在⊙O上,连接PD、BD,已知PC=PD=BC.下列结论:
①PD与⊙O相切;
②四边形PCBD是菱形;
③PO=AB;
④∠PDB=120°.
其中,正确的个数是( )
A.4个
B.3个
C.2个
D.1个
【答案】A
【解析】解:①连接CO,DO,
∵PC与⊙O相切,切点为C,
∴∠PCO=90°,
在△PCO和△PDO中,
∵  ,
,
∴△PCO≌△PDO(SSS),
∴∠PCO=∠PDO=90°,
∴PD与⊙O相切,
故①正确;
②由①得:∠CPB=∠BPD,
在△CPB和△DPB中,
∵  ,
,
∴△CPB≌△DPB(SAS),
∴BC=BD,
∴PC=PD=BC=BD,
∴四边形PCBD是菱形,
故②正确;
③连接AC,
∵PC=CB,
∴∠CPB=∠CBP,
∵AB是⊙O直径,
∴∠ACB=90°,
在△PCO和△BCA中,
∵  ,
,
∴△PCO≌△BCA(ASA),
∴AC=CO,
∴AC=CO=AO,
∴∠COA=60°,
∴∠CPO=30°,
∴CO= ![]() PO=
PO= ![]() AB,
AB,
∴PO=AB,
故③正确;
④∵四边形PCBD是菱形,∠CPO=30°,
∴DP=DB,则∠DPB=∠DBP=30°,
∴∠PDB=120°,
故④正确;
正确个数有4个,
故答案为:A.
①连接CO,DO,在△PCO和△PDO中,根据边边边可得△PCO≌△PDO,由全等三角形的性质可得∠PCO=∠PDO=90°,根据切线的判断可得PD与⊙O相切,则①符合题意;在△CPB和△DPB中,根据边角边可证△CPB≌△DPB,则BC=BD,结合已知条件可得PC=PD=BC=BD,由菱形的判定可得四边形PCBD是菱形,所以②符合题意;在△PCO和△BCA中,用角边角可证△PCO≌△BCA,由全等三角形的性质可得AC=CO,那么有AC=CO=AO,所以∠COA=60°,∠CPO=30°,根据直角三角形中,30度角所对的直角边等于斜边的一半可得CO= ![]() PO=
PO= ![]() AB,所以PO=AB,故③符合题意;根据四边形PCBD是菱形可得DP=DB,结合∠CPO=30°可得∠DPB=∠DBP=30°,则∠PDB=120°,所以④符合题意。所以符合题意的选项是A。
AB,所以PO=AB,故③符合题意;根据四边形PCBD是菱形可得DP=DB,结合∠CPO=30°可得∠DPB=∠DBP=30°,则∠PDB=120°,所以④符合题意。所以符合题意的选项是A。

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案