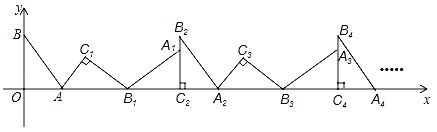
题目内容
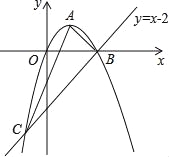
【题目】(2016广西省南宁市第24题)如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x﹣2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求证:△ABC是直角三角形;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)、y=﹣x2+2x;C(-1,-3);(2)、证明过程见解析;(3)、(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0)
,0)或(﹣1,0)或(5,0)
【解析】
试题分析:(1)、可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;(2)、分别过A、C两点作x轴的垂线,交x轴于点D、E两点,结合A、B、C三点的坐标可求得∠ABO=∠CBO=45°,可证得结论;(3)、设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得![]() =
=![]() 或
或![]() =
=![]() ,可求得N点的坐标.
,可求得N点的坐标.
试题解析:(1)、∵顶点坐标为(1,1), ∴设抛物线解析式为y=a(x﹣1)2+1,
又抛物线过原点, ∴0=a(0﹣1)2+1,解得a=﹣1, ∴抛物线解析式为y=﹣(x﹣1)2+1, 即y=﹣x2+2x,
联立抛物线和直线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(2,0),C(﹣1,﹣3);
(2)、如图,分别过A、C两点作x轴的垂线,交x轴于点D、E两点,
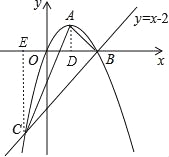
则AD=OD=BD=1,BE=OB+OE=2+1=3,EC=3, ∴∠ABO=∠CBO=45°,即∠ABC=90°, ∴△ABC是直角三角形;
(3)、假设存在满足条件的点N,设N(x,0),则M(x,﹣x2+2x),
∴ON=|x|,MN=|﹣x2+2x|, 由(2)在Rt△ABD和Rt△CEB中,可分别求得AB=![]() ,BC=3
,BC=3![]() ,
,
∵MN⊥x轴于点N ∴∠ABC=∠MNO=90°, ∴当△ABC和△MNO相似时有![]() =
=![]() 或
或![]() =
=![]() ,
,
①当![]() =
=![]() 时,则有
时,则有![]() =
=![]() ,即|x||﹣x+2|=
,即|x||﹣x+2|=![]() |x|,
|x|,
∵当x=0时M、O、N不能构成三角形, ∴x≠0, ∴|﹣x+2|=![]() ,即﹣x+2=±
,即﹣x+2=±![]() ,解得x=
,解得x=![]() 或x=
或x=![]() ,
,
此时N点坐标为(![]() ,0)或(
,0)或(![]() ,0);
,0);
②当![]() =
=![]() 时,则有
时,则有![]() =
=![]() ,即|x||﹣x+2|=3|x|,
,即|x||﹣x+2|=3|x|,
∴|﹣x+2|=3,即﹣x+2=±3,解得x=5或x=﹣1, 此时N点坐标为(﹣1,0)或(5,0),
综上可知存在满足条件的N点,其坐标为(![]() ,0)或(
,0)或(![]() ,0)或(﹣1,0)或(5,0).
,0)或(﹣1,0)或(5,0).

 小学教材完全解读系列答案
小学教材完全解读系列答案