题目内容
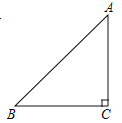
【题目】在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
【答案】C
【解析】试题解析:分为两种情况:
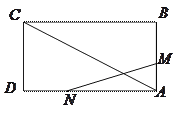
①如图1,当CE在△ABC内.
∵AD⊥CE,∠BCA=90°,
∴∠ADC=∠BCA=90°,
∴∠DCA+∠BCE=90°,∠DCA+∠DAC=90°,
∴∠DAC=∠BCE,
∵AD⊥CE,BE⊥CE,
∴∠ADC=∠BEC=90°,
在△ACD和△CBE中,
 ,
,
∴△ACD≌△CBE(AAS)
∴CE=AD=2cm,CD=BE,
BE=CD=CE+DE=2cm+4cm=6cm;
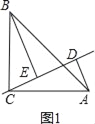
②如图2,当CE在△ABC外.

∵在△EBC和△DAC中,
 ,
,
∴△ACD≌△CBE(AAS),
∴CE=AD=2cm,BE=CD,
∴BE=CD=DE﹣AD=4cm﹣2cm=2cm,
故答案为:6或2.
故选C.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目