题目内容
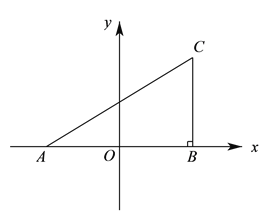
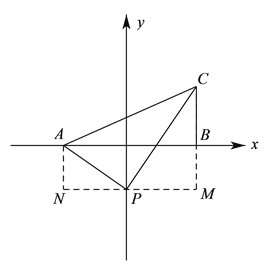
【题目】如图①,在平面直角坐标系中, ![]() ,
, ![]() ,且满足
,且满足![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 和
和![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
(![]() )动点
)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿射线
的速度沿射线![]() 运动,如果在运动过程中
运动,如果在运动过程中![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 运动的时间.
运动的时间.
【答案】见解析.
【解析】试题分析:(1)根据非负数的性质易得a=-2,b=2,然后根据三角形面积公式计算即可;(2)分①当![]() 点在
点在![]() 轴正半轴上时和②当
轴正半轴上时和②当![]() 点在
点在![]() 轴负半轴上时两种情况求点P的坐标;(3)可分①当
轴负半轴上时两种情况求点P的坐标;(3)可分①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时三种情况求点
时三种情况求点![]() 运动的时间.
运动的时间.
试题解析:
(![]() )∵
)∵![]() ,
,
![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∵![]() 轴于点
轴于点![]() .
.
∴![]() .
.
∴![]() .
.
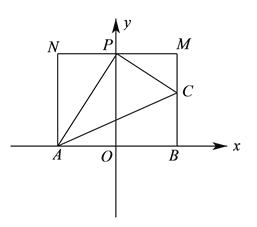
(![]() )①当
)①当![]() 点在
点在![]() 轴正半轴上时,设
轴正半轴上时,设![]() .
.
∴![]() .
.
如图所示,过![]() 作
作![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴.
轴.
∴![]() ,
,
![]() .
.
∴![]()
![]()
![]()
![]() .
.
解得![]() .
.
∴![]() .
.
②当![]() 点在
点在![]() 轴负半轴上时,设
轴负半轴上时,设![]() .
.
∴![]() .
.
如图所示,过![]() 作
作![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴.
轴.
∴![]() ,
,
![]() .
.
![]() .
.
∴![]()
![]()
![]()
![]() .
.
解得![]() .
.
∴![]() ,
,
综上, ![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(![]() )①当
)①当![]() 时,
时,
![]() .
.
∴![]() .
.
②当![]() 时,
时,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
③当![]() 时,
时,
设![]() .
.
∴![]() .
.
在![]() 中,
中, ![]() .
.
∴![]() .
.
解得![]() .
.
∴![]() ,
,
∴![]() .
.
综上![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目