题目内容
如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连结BC．若∠A＝
36°，则∠C= ▲ ．
36°，则∠C= ▲ ．
连接根据三角形的内角和定理就得到关于∠C的方程，从而求出．
解：设AC与⊙O的另一交点为D，连接BD，
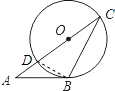
则∠DBC=90°，
设∠C=x，
则∠ABD=x，∠BDC=∠A+∠DBA=36°+x；
∵∠CDB+∠C=90°，
∴36°+x+x=90°，
解得x=27°
解：设AC与⊙O的另一交点为D，连接BD，
则∠DBC=90°，
设∠C=x，
则∠ABD=x，∠BDC=∠A+∠DBA=36°+x；
∵∠CDB+∠C=90°，
∴36°+x+x=90°，
解得x=27°
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
中，
，
，
的圆心为
，如果图中两个阴影部分的面积相等，那么
的长是 .（结果保留
)
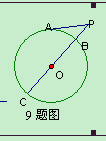
的圆形纸片折叠后，圆弧恰好经过圆心
，则折痕
的
．
是⊙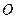
的弦，点D是弧AB的中点，过B作A
B的垂线交AD的延长线于C．求证：AD＝DC．
和
的半径分别是5和4，
，则
得到△AED，AE交半圆于点F，连接DF。