题目内容
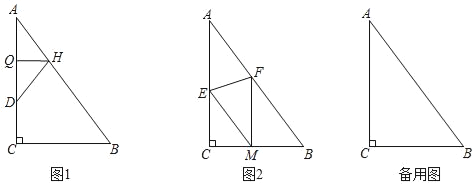
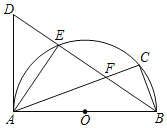
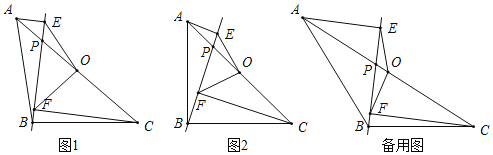
【题目】在△ABC中,AB=BC,点O是AC的中点,点P是AC上的一个动点(点P不与点A,O,C重合).过点A,点C作直线BP的垂线,垂足分别为点E和点F,连接OE,OF.
(1)如图1,请直接写出线段OE与OF的数量关系;
(2)如图2,当∠ABC=90°时,请判断线段OE与OF之间的数量关系和位置关系,并说明理由
(3)若|CF﹣AE|=2,EF=2![]() ,当△POF为等腰三角形时,请直接写出线段OP的长.
,当△POF为等腰三角形时,请直接写出线段OP的长.
【答案】(1)OF =OE;(2)OF⊥EK,OF=OE,理由见解析;(3)OP的长为![]() 或
或![]() .
.
【解析】(1)如图1中,延长EO交CF于K,证明△AOE≌△COK,从而可得OE=OK,再根据直角三角形斜边中线等于斜边一半即可得OF=OE;
(2)如图2中,延长EO交CF于K,由已知证明△ABE≌△BCF,△AOE≌△COK,继而可证得△EFK是等腰直角三角形,由等腰直角三角形的性质即可得OF⊥EK,OF=OE;
(3)分点P在AO上与CO上两种情况分别画图进行解答即可得.
(1)如图1中,延长EO交CF于K,
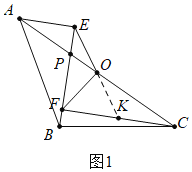
∵AE⊥BE,CF⊥BE,∴AE∥CK,∴∠EAO=∠KCO,
∵OA=OC,∠AOE=∠COK,∴△AOE≌△COK,∴OE=OK,
∵△EFK是直角三角形,∴OF=![]() EK=OE;
EK=OE;
(2)如图2中,延长EO交CF于K,
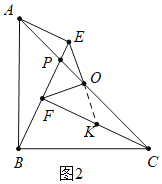
∵∠ABC=∠AEB=∠CFB=90°,
∴∠ABE+∠BAE=90°,∠ABE+∠CBF=90°,∴∠BAE=∠CBF,
∵AB=BC,∴△ABE≌△BCF,∴BE=CF,AE=BF,
∵△AOE≌△COK,∴AE=CK,OE=OK,∴FK=EF,
∴△EFK是等腰直角三角形,∴OF⊥EK,OF=OE;
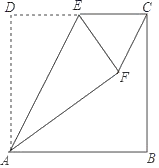
(3)如图3中,点P在线段AO上,延长EO交CF于K,作PH⊥OF于H,
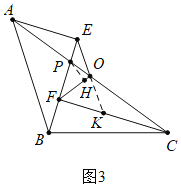
∵|CF﹣AE|=2,EF=2![]() ,AE=CK,∴FK=2,
,AE=CK,∴FK=2,
在Rt△EFK中,tan∠FEK=![]() ,∴∠FEK=30°,∠EKF=60°,
,∴∠FEK=30°,∠EKF=60°,
∴EK=2FK=4,OF=![]() EK=2,
EK=2,
∵△OPF是等腰三角形,观察图形可知,只有OF=FP=2,
在Rt△PHF中,PH=![]() PF=1,HF=
PF=1,HF=![]() ,OH=2﹣
,OH=2﹣![]() ,
,
∴OP=![]() .
.
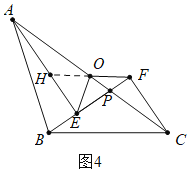
如图4中,点P在线段OC上,当PO=PF时,∠POF=∠PFO=30°,
∴∠BOP=90°,
∴OP=![]() OE=
OE=![]() ,
,
综上所述:OP的长为![]() 或
或![]() .
.

 阅读快车系列答案
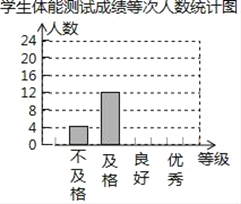
阅读快车系列答案【题目】某校为了解学生体质情况,从各年级随机抽取部分学生进行体能测试,每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级,统计员在将测试数据绘制成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如图图表,请按正确数据解答下列各题:
学生体能测试成绩各等次人数统计表
体能等级 | 调整前人数 | 调整后人数 |
优秀 | 8 |
|
良好 | 16 |
|
及格 | 12 |
|
不及格 | 4 |
|
合计 | 40 |
|
(1)填写统计表;
(2)根据调整后数据,补全条形统计图;
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.