��Ŀ����
����Ŀ����ͼ�٣���ƽ��ֱ������ϵ�У�������y=-![]() x2-
x2-![]() x-3��x����A��B����(��A�ڵ�B�����)����y���ڵ�C.
x-3��x����A��B����(��A�ڵ�B�����)����y���ڵ�C.

(1)��ֱ��AC�Ľ���ʽ��
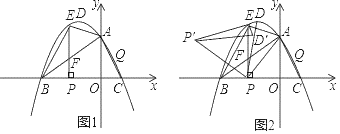
(2)�ٵ�P��ֱ��AC�Ϸ��������ϵ�һ������(�����A����C�غ�)������P��PD��AC�ڵ�D����PD�����ֵ��
�ڵ��߶�PD�ij������ʱ����Q�ӵ�P����������ÿ��1����λ���ȵ��ٶ����ʵ���·���˶���y���ϵĵ�M��������MC��ÿ��![]() ����λ���ȵ��ٶ��˶�����Cֹͣ������Q�������˶���������ʱ����ʱ�����M�����ꣻ
����λ���ȵ��ٶ��˶�����Cֹͣ������Q�������˶���������ʱ����ʱ�����M�����ꣻ
(3)��ͼ�ڣ�����BOC��ֱ��BCƽ�ƣ���Bƽ�ƺ�Ķ�Ӧ��Ϊ��B'����Oƽ�ƺ�Ķ�Ӧ��Ϊ��O'����Cƽ�ƺ�Ķ�Ӧ��Ϊ��C'����S������ƽ����һ�㣬����A��C��O'��SΪ������ı��������Σ�������з��������ĵ�O'������.
���𰸡�(1)y=-![]() x-3��(2)��PD=
x-3��(2)��PD=![]() ����M(0��2)��(3)���������ĵ�O'������Ϊ(
����M(0��2)��(3)���������ĵ�O'������Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��-9)��(-
)��(3��-9)��(-![]() ��
��![]() )��(
)��(![]() ��
��![]() ).
).
��������
(1)�ֱ����������y=-![]() x2-
x2-![]() x-3��x�ᡢy��Ľ������꣬Ȼ��ֱ��A(-6��0)�� C(0��-3)����ֱ��AC�Ľ���ʽΪy=kx+b �У����Ԫһ�η����鼴��.
x-3��x�ᡢy��Ľ������꣬Ȼ��ֱ��A(-6��0)�� C(0��-3)����ֱ��AC�Ľ���ʽΪy=kx+b �У����Ԫһ�η����鼴��.
(2)������AC=3![]() Ϊ��ֵ�����������ε������ʽ����֪����PAC��������ʱ��PD���ʱ�����������ε������ʽ����Ĺ�ϵʽ�����ö��κ��������������PAC��������ֵΪ
Ϊ��ֵ�����������ε������ʽ����֪����PAC��������ʱ��PD���ʱ�����������ε������ʽ����Ĺ�ϵʽ�����ö��κ��������������PAC��������ֵΪ![]() ������S��PAC=
������S��PAC=![]() AC��PD���������PD�ij�.
AC��PD���������PD�ij�.
�����ù��ɶ��������CN=![]() ������sin��OCN=
������sin��OCN=![]() �������MK=
�������MK=![]() �� �Ӷ��ɵõ�Q�������˶������е�ʱ�����PK�ij�������P��PE��y���ڵ�E�����ݴ��߶���̿�֪��y�ύ�㼴ΪM��sin��OCN=sin��EPM=
�� �Ӷ��ɵõ�Q�������˶������е�ʱ�����PK�ij�������P��PE��y���ڵ�E�����ݴ��߶���̿�֪��y�ύ�㼴ΪM��sin��OCN=sin��EPM=![]() ���Ӷ����OM=2������M������.
���Ӷ����OM=2������M������.
(3)����ͼ�ۡ�ͼ���������ε���������ȣ��ɵ�AC=AO'=3![]() �����ݵ�O'��ֱ��y=-3x�ϣ���O'(m��-3m)�����ù��ɶ���������ʽ�����m����.
�����ݵ�O'��ֱ��y=-3x�ϣ���O'(m��-3m)�����ù��ɶ���������ʽ�����m����.
����ͼ�ݡ�ͼ�ޣ�ͬ�ٿɵ�.
����ͼ�ߣ�ͬ�ٿɵ�.
(1)�⣺����������y=-![]() x2-
x2-![]() x-3����x=0���õ�y=-3��
x-3����x=0���õ�y=-3��
��C(0��-3)��
��y=0���õ�x2+7x+6=0�����x=-6��x=-1��
��A(-6��0)��B(-1��0)��
��ֱ��AC�Ľ���ʽΪy=kx+b������ 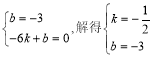 ��
��
��ֱ��AC�Ľ���ʽΪy=-![]() x-3.
x-3.
(2)�⣺����ͼ�٣�
��P(m��-![]() m2-
m2-![]() m-3)������PA��PC����PK��y�ύAC�ڵ�K����K(m��-
m-3)������PA��PC����PK��y�ύAC�ڵ�K����K(m��-![]() m-3)��
m-3)��
��PD��AC��AC=3![]() Ϊ��ֵ��
Ϊ��ֵ��
��PD���ʱ����PAC��������
��S��PAC=![]() ��(-
��(-![]() m2-3m)��6=-
m2-3m)��6=-![]() (m+3)2+
(m+3)2+![]() ��
��
��m=-3ʱ����PAC�����������ֵΪ![]() ����ʱP(-3��3)��
����ʱP(-3��3)��![]() ��AC��PD=
��AC��PD=![]() ��
��
��PD=![]() .
.
����ͼ�ڣ�
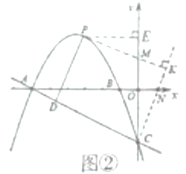
��x����ȡһ��N(1��0)����ֱ��CN������P��PK��CN�ڵ�K����y���ڵ�M.
��OC=3��ON=1��
��CN= ![]() ��
��
��sin��OCN=![]() ��
��
��MK=![]() ��
��
��.��Q�������˶������е�ʱ��=![]() =PM+MK=PK��
=PM+MK=PK��
���ݴ��߶���̿�֪����M��Ϊ����ĵ㣬����P��PE��y���ڵ�E��![]() ��
��
��EM=1��
��OM=2��
��M(0��2)
(3)�⣺����ͼ�ۡ�ͼ�ܣ�
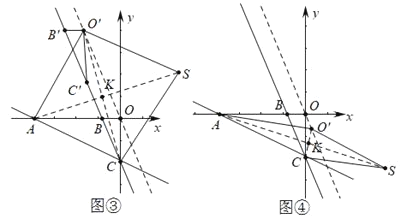
���ı���ACSO'������ʱ����AS��CO'�ڵ�K��AC=AO'=3![]() ��
��
�ߵ�O'��ֱ��y=-3x�ϣ�A(-6��0)����O'(m��-3m)��
��(m+6)2+(-3m)2=(3![]() )2�����m=
)2�����m= ![]() ��
��
��O'(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��
)��
����ͼ�ݡ�ͼ�ޣ�
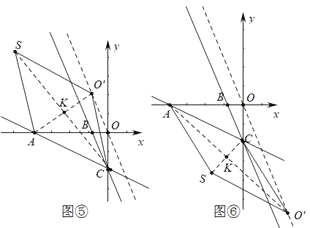
���ı���ACO'S������ʱ����CS��AO'�ڵ�K��AC=CO'=3![]() ��
��
�ߵ�O'��ֱ��y=-3x�ϣ�C(0��-3)����O'(m��-3m)��
��m2+(-3m+3)2=(3![]() )2�����m=3��m=-
)2�����m=3��m=-![]() ��
��
��O'(3��-9)��(-![]() ��
��![]() ).
).
����ͼ�ߣ�
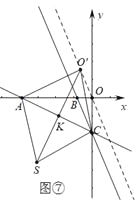
���ı���ASCO'������ʱ����AC��SO'�ڵ�K��AC=3![]() .
.
�ߵ�O'��ֱ��y=-3x�ϣ�C(0��-3)����O'(m��-3m)��
��m2+(-3m+3)2=(![]() )2+(m+3)2
)2+(m+3)2![]() )�����m=
)�����m=![]() ��
��
��O'(![]() ��
��![]() )��
)��
�������������������ĵ�O'������Ϊ(![]() ��
��![]() )��(
)��(![]() ��
��![]() )��(3��-9)��(-
)��(3��-9)��(-![]() ��
��![]() )��(
)��(![]() ��
��![]() ).
).

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�