题目内容
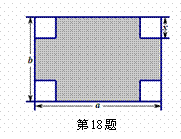
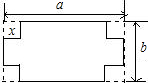 如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.(1)用a,b,x表示剩余部分的面积;
(2)当a=8,b=6,且剪去的面积等于剩余部分的面积的一半时,求正方形的边长x.
分析:(1)剩余部分的面积=原矩形的面积-四个小正方形的面积;
(2)根据剪去的面积等于剩余部分的面积的一半,可得4x2=
(ab-4x2),把a=8,b=6代入即可求得x的值.
(2)根据剪去的面积等于剩余部分的面积的一半,可得4x2=
| 1 |
| 2 |
解答:解:(1)剩余部分的面积S=ab-4x2;
(2)由剪去的面积等于剩余部分的面积的一半,得4x2=
(ab-4x2),
把a=8,b=6代入,得4x2=
(ab-4x2),
解得x=2.
∴正方形的边长x=2.
(2)由剪去的面积等于剩余部分的面积的一半,得4x2=
| 1 |
| 2 |
把a=8,b=6代入,得4x2=
| 1 |
| 2 |
解得x=2.
∴正方形的边长x=2.
点评:此题主要考查用代数式表示正方形、矩形的面积,需熟记公式,且认真观察图形,得出等量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
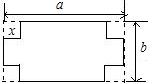 如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.
如图,在长和宽分别是a、b的矩形纸片的四个角都剪去一个边长为x的正方形.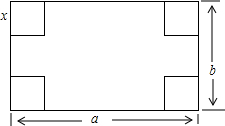 如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的
如图,在长和宽分别是a、b的长方纸片的四个角都剪去一个边长为x的正方形,当a=8,b=6,且剪去部分的面积等于剩余部分的面积的 时,求正方形的边长x的值.
时,求正方形的边长x的值.