Question

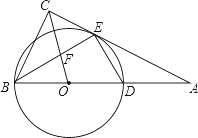
【题目】如图，正方形ABCD的对角线AC和BD相交于点O，正方形A1B1C1O的边OA1交AB于点E，OC1交BC于点F．

（1）求证：（BE+BF）2=2OB2；

（2）如果正方形ABCD的边长为a，那么正方形A1B1C1O绕O点转动的过程中，与正方形ABCD重叠部分的面积始终等于　　　　 （用含a的代数式表示）

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

（1）由题意得OA=OB，∠OAB=∠OBC=45°又因为∠AOE+∠EOB=90°，∠BOF+∠EOB=90°可得∠AOE=∠BOF，根据ASA可证△AOE≌△BOF，可得AE=BF，可得BE+BF=AB，由勾股定理可得结论；

（2）由全等三角形的性质可得S△AOE=S△BOF，可得重叠部分的面积为正方形面积的，即可求解．

解：（1）在正方形ABCD中，AO=BO，∠AOB=90°，∠OAB=∠OBC=45°．

∵∠AOE+∠EOB=90°，∠BOF+∠EOB=90°，∴∠AOE=∠BOF．

在△AOE和△BOF中

，

∴△AOE≌△BOF（ASA），

∴AE=BF，

∴BE+EF=BE+AE=AB

在Rt△AOB中，AB2=OA2+OB2，且OA=OB，

∴（BE+BF）2=2OB2，

（2）∵△AOE≌△BOF，

∴S△AOE=S△BOF，

∴重叠部分的面积=S△AOB=S正方形ABCD=a2．

故答案为：a2．