题目内容
【题目】综合与实践
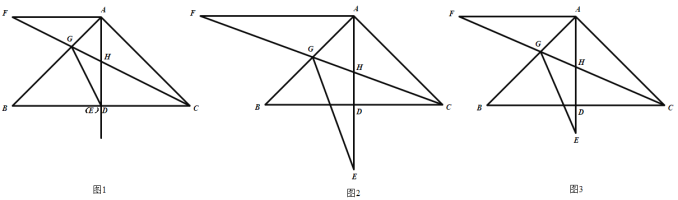
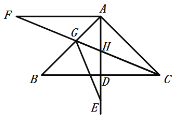
问题情境:△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,点E是射线AD上的一个动点(不与点A重合)将线段AE绕点A顺时针旋转90°得到线段AF,连接CF交线段AB于点G,交AD于点H、连接EG.
特例分析:
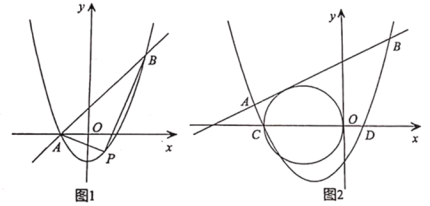
(1)如图1,当点E与点D重合时,“智敏”小组提出如下问题,请你解答:
①求证:AF=CD;
②用等式表示线段CG与EG之间的数量关系为:_______;
拓展探究:
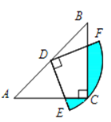
(2)如图2,当点E在线段AD的延长线上,且DE=AD时,“博睿”小组发现CF=2EG.请你证明;
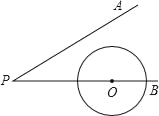
(3)如图3,当点E在线段AD的延长线上,且AE=AB时,![]() 的值为_______;
的值为_______;
推广应用:
(4)当点E在射线AD上运动时,![]() ,则
,则![]() 的值为______用含m.n的式子表示).
的值为______用含m.n的式子表示).
【答案】(1)①见解析;②CG=2EG;(2)见解析;(3)![]() ;(4)
;(4)![]()
【解析】
(1)①根据等腰直角三角形的性质证得AD=CD,再证明△AFG![]() △ADG,即可证明结论;
△ADG,即可证明结论;
②根据①得到BC=2AF,FG=GD,再证明△AFG![]() △BCG,即可得到CG=2EG;
△BCG,即可得到CG=2EG;
(2)先证得四边形ABEC为正方形,同理得△AFG![]() △AEG和△AFG
△AEG和△AFG![]() △BCG,即可得证;
△BCG,即可得证;
(3)根据等腰直角三角形的性质得到![]() ,证得△AFG
,证得△AFG![]() △BCG,即可求解;
△BCG,即可求解;
(4) 根据等腰直角三角形的性质得到BC=2AD,继而得到![]() ,由△AFG
,由△AFG![]() △BCG,即可求解.
△BCG,即可求解.
(1)①△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D,
∴AD=BD=CD=![]() BC,∠BAD=∠CAD=45°,
BC,∠BAD=∠CAD=45°,
根据旋转的性质得:AF=AD,∠DAF=90°,
∴∠GAF=∠GAD=45°,
在△AFG和△ADG中,
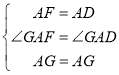 ,
,
∴△AFG![]() △ADG,
△ADG,
∴AF=AD,
∴AF=CD;
②CG=2EG,理由如下:
由①得:∠GAF=∠B=45°,AF=![]() BC,
BC,
∴AF∥BC,2AF=BC,
∴△AFG![]() △BCG,
△BCG,
∴![]() ,
,
∴CG=2FG,
∵△AFG![]() △ADG,
△ADG,
∴FG=DG,即FG=EG,
∴CG=2EG;
(2) 连接EB、EC,
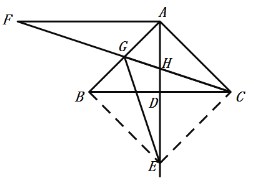
∵∠BAC=90°,AB=AC,AD⊥BC于点D,DE=AD,
∴DE=AD=BD=CD,且AE⊥BC,∠BAC=90°,
∴四边形ABEC为正方形,
∴BC=AE,
根据旋转的性质得:AF=AE,∠EAF=90°,
∴∠GAF=∠GAE=45°,
在△AFG和△AEG中,
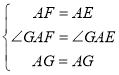 ,
,
∴△AFG![]() △AEG,
△AEG,
∴AF=AE=BC,FG= EG,
在△AFG和△BCG中,
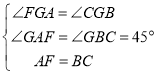 ,
,
∴△AFG![]() △BCG,
△BCG,
∴FG= CG,
∴FG= CG= EG,
∴CF=2EG;
(3) 同理得:FG= EG,
△ABC中,∠BAC=90°,AB=AC,
∴![]() ,即
,即![]() ,
,
同理得:△AFG![]() △BCG,
△BCG,
∴![]() ,
,
∴![]() ,
,
∴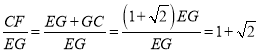 ,
,
∴![]() ;
;
(4)同理可得:FG= EG,BC=2AD,AF=AE,
∵![]() ,
,
∴![]() ,
,
同理可得:△AFG![]() △BCG,
△BCG,
∴![]() ,
,
∴![]() ,
,
∴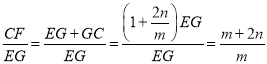 ,
,
∴![]() ;
;

 阶梯计算系列答案
阶梯计算系列答案