题目内容
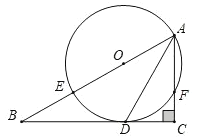
【题目】如图,点A在反比例函数![]() (x<0)的图象上,连接OA,分别以点O和点A为圆心,大于
(x<0)的图象上,连接OA,分别以点O和点A为圆心,大于![]() 的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
的长为半径作弧,两弧相交于B,C两点,过B,C两点作直线交x轴于点D,连接AD.若∠AOD=30°,△AOD的面积为2,则k的值为( )
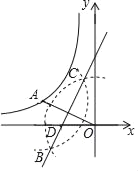
A.﹣6B.6C.﹣2D.﹣3
【答案】A
【解析】
过A作AE⊥x轴于E,根据BC垂直平分AO,即可得到AD=OD,S△ADF=S△ODF=1,进而得出△ADE≌△ADF(AAS),可得S△AOE=3,再根据反比例函数系数k的几何意义,即可得到k的值.
解:如图,过A作AE⊥x轴于E,
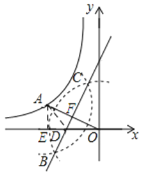
依据作图可得,BC垂直平分AO,
∴AD=OD,S△ADF=S△ODF=1,
∴∠AOD=∠OAD=30°,
∴∠ADE=60°,
∴∠DAE=∠DAF=30°,
又∵∠AED=∠AFD=90°,AD=AD,
∴△ADE≌△ADF(AAS),
∴S△AOE=3,
∵点A在反比例函数y=![]() (x<0)的图象上,
(x<0)的图象上,
∴![]() |k|=3,
|k|=3,
解得k=±6,
又∵k<0,
∴k=-6,
故选A.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目