题目内容
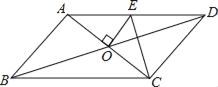
【题目】如图，平行四边形ABCD的对角线相交于点O，且AD＞AB，过点O作OE⊥AC交AD于点E，连接CE．若平行四边形ABCD的周长为20，则△CDE的周长是（ ）
A. 10B. 11C. 12D. 13
【答案】A
【解析】
由平行四边形ABCD的对角线相交于点O，OE⊥AC，根据线段垂直平分线的性质，可得AE=CE，又AB+BC=AD+CD=20，继而可得△CDE的周长等于AD+CD．
∵四边形ABCD是平行四边形，
∴OA＝OC，AB＝CD，AD＝BC，
∵平行四边形ABCD的周长为20，
∴AD+CD＝10，
∵OE⊥AC，
∴AE＝CE，
∴△CDE的周长为：CD+CE+DE＝CD+CE+AE＝AD+CD＝10．
故选A．
练习册系列答案
阳光课堂课时优化作业系列答案
相关题目
【题目】前不久在台湾抗震救灾中，某地将甲、乙两个仓库的粮食全部转移到A、B两个仓库．甲库有粮食100吨，乙库有粮食80吨，而A库的容量为70吨，B库的容量为110吨．从甲、乙两库到A，B两库的路程和运费如下表：
路程（km） | 运费（元/吨km） | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A库 | 20 | 15 | 12 | 12 |
B库 | 25 | 20 | 10 | 8 |
（1）若甲库运往A库粮食x吨，请写出将粮食运往A、B两库的总运费y（元）与x（吨）函数关系式．
（2）当甲、乙两库各运往A、B两库多少吨粮食时，总运费最省，最省的总运费是多少？
