题目内容
【题目】如图,等边△ABC的边长为10,点M是边AB上一动点,将等边△ABC沿过点M的直线折叠,该直线与直线AC交于点N,使点A落在直线BC上的点D处,且BD:DC=1:4,折痕为MN,则AN的长为 . 
【答案】7或 ![]()
【解析】解:①当点A落在如图1所示的位置时,
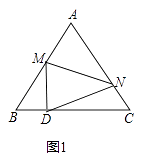
∵△ACB是等边三角形,
∴∠A=∠B=∠C=∠MDN=60°,
∵∠MDC=∠B+∠BMD,∠B=∠MDN,
∴∠BMD=∠NDC,
∴△BMD∽△CDN.
∴得 ![]() =
= ![]() =
= ![]() ,
,
∵DN=AN,
∴得 ![]() =
= ![]() =
= ![]() ,
,
∵BD:DC=1:4,BC=10,
∴DB=2,CD=8,
设AN=x,则CN=10﹣x,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴DM= ![]() ,BM=
,BM= ![]() ,
,
∵BM+DM=30,
∴ ![]() +
+ ![]() =10,
=10,
解得x=7,
∴AN=7;
②当A在CB的延长线上时,如图2,
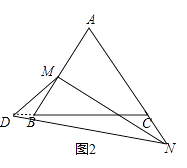
与①同理可得△BMD∽△CDN.
∴得 ![]() =
= ![]() =
= ![]() ,
,
∵BD:DC=1:4,BC=10,
∴DB= ![]() ,CD=
,CD= ![]() ,
,
设AN=x,则CN=x﹣10,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴DM= ![]() ,BM=
,BM= ![]() ,
,
∵BM+DM=10,
∴ ![]() +
+ ![]() =10,
=10,
解得:x= ![]() ,
,
∴AN= ![]() .
.
所以答案是:7或 ![]() .
.
【考点精析】通过灵活运用翻折变换(折叠问题)和相似三角形的判定与性质,掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目