��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У�������OABC�Ķ���B�ڵ�һ���ޣ�����A��C�ֱ���x���y���ϣ�ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E���Ե�EΪ�����������K������B��6��6����
��1����������K�Ľ���ʽ��
��2����P���߶�OC��һ�㣬��O����AP�ĶԳƵ�ΪM��
������M����ֱ��l1��l2��ʱ�������������»�����ƽ�ƶ��٣�ʹ�䶥������AM�ϣ�
������M�����������ϣ���ֱ��д��һ����������ĵ�P�����꣮
���𰸡�
��1����: ��ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�E��
���E��������4��4����
��������K�Ľ���ʽΪy=a��x��4��2+4��
��������K������B��6��6����
��6=a��6��4��2+4��
��ã�a= ![]() ��
��
��������K�Ľ���ʽΪy= ![]() ��x��4��2+4
��x��4��2+4
��2����: ����AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2��
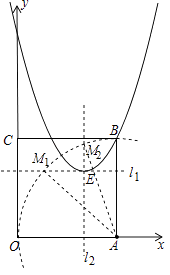
��M1��m��4����M2��4��n����
��A��6��0����OM=6��
�ࣨm��6��2+42=62����4��6��2+n2=62��
���m=6��2 ![]() ��n=4
��n=4 ![]() ��
��
��M��6��2 ![]() ��4����
��4����
�� ![]() =
= ![]() ��
��
��ã�h1= ![]() ��
��
�ཫ����������ƽ��4�� ![]() ��ʹ�䶥������AM1�ϣ�������������ƽ��4
��ʹ�䶥������AM1�ϣ�������������ƽ��4 ![]() ��4��ʹ�䶥������AM2��
��4��ʹ�䶥������AM2��
�ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
����������1�������ҳ�E������꣬���ô���ϵ����������⣻��2������AΪԲ�ģ���6Ϊ�뾶��������ֱ��l1��x=4��ֱ��l2��y=4�ཻ�ڵ�M1��M2����M1��m��4����M2��4��n�����ɹ��ɶ����ó�����m��n�ķ��̣��ⷽ�̼��ɣ��ڵ���P���C�غ�ʱ����M��B�غϣ���M���������ϣ���ʱP��0��6����
�����㾫����ͨ��������ö��κ���ͼ���ƽ�ƺ������ε����ʣ�����ƽ�Ʋ��裺��1���䷽ y=a(x-h)2+k��ȷ�����㣨h,k����2����x������Ҽ�����y���ϼ��¼����������ĸ��Ƕ���ֱ�ǣ������߶���ȣ������ε������Խ�����ȣ����һ��ഹֱƽ�֣�ÿ���Խ���ƽ��һ��Խǣ������ε�һ���Խ��߰������ηֳ�����ȫ�ȵĵ���ֱ�������Σ������εĶԽ�����ߵļн���45o�������ε������Խ��߰���������ηֳ��ĸ�ȫ�ȵĵ���ֱ�������μ����Խ����⣮