题目内容
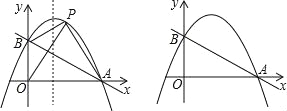
【题目】如图,直线y=﹣![]() x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
x+1与x轴交于点A,与y轴交于点B,抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的一点,连接PA、PB、PO,若△POA的面积是△POB面积的![]() 倍.
倍.
①求点P的坐标;
②点Q为抛物线对称轴上一点,请直接写出QP+QA的最小值;
(3)点M为直线AB上的动点,点N为抛物线上的动点,当以点O、B、M、N为顶点的四边形是平行四边形时,请直接写出点M的坐标.
【答案】(1) y=﹣x2+![]() x+1;(2)①P(
x+1;(2)①P(![]() ,1);②
,1);②![]() ;(3)满足条件的点M的坐标(1+
;(3)满足条件的点M的坐标(1+![]() ,
,![]() (1﹣
(1﹣![]() ))或(1﹣
))或(1﹣![]() ,﹣
,﹣![]() (1+
(1+![]() ))或(1,
))或(1,![]() )或M(﹣(1+
)或M(﹣(1+![]() ),
),![]() (3+
(3+![]() ))或M(﹣(1﹣
))或M(﹣(1﹣![]() ),
),![]() (3﹣
(3﹣![]() )).
)).
【解析】
试题分析:(1)先确定出点A,B坐标,再用待定系数法求出抛物线解析式;(2)设出点P的坐标,①用△POA的面积是△POB面积的![]() 倍,建立方程求解即可;②利用对称性找到最小线段,用两点间距离公式求解即可;(3)分OB为边和为对角线两种情况进行求解,①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.
倍,建立方程求解即可;②利用对称性找到最小线段,用两点间距离公式求解即可;(3)分OB为边和为对角线两种情况进行求解,①当OB为平行四边形的边时,用MN∥OB,表示和用MN=OB,建立方程求解;②当OB为对角线时,OB与MN互相平分,交点为H,设出M,N坐标用OH=BH,MH=NH,建立方程组求解即可.
试题解析:(1)∵直线y=﹣![]() x+1与x轴交于点A,与y轴交于点B,
x+1与x轴交于点A,与y轴交于点B,
∴A(2,0),B(0,1),
∵抛物线y=﹣x2+bx+c经过A、B两点,
∴![]() ,
,
∴![]()
∴抛物线解析式为y=﹣x2+![]() x+1,
x+1,
(2)①由(1)知,A(2,0),B(0,1),
∴OA=2,OB=1,
由(1)知,抛物线解析式为y=﹣x2+![]() x+1,
x+1,
∵点P是第一象限抛物线上的一点,
∴设P(a,﹣a2+![]() a+1),((a>0,﹣a2+
a+1),((a>0,﹣a2+![]() a+1>0),
a+1>0),
∴S△POA=![]() OA×Py=
OA×Py=![]() ×2×(﹣a2+
×2×(﹣a2+![]() a+1)=﹣a2+
a+1)=﹣a2+![]() a+1
a+1
S△POB=![]() OB×Px=
OB×Px=![]() ×1×a=
×1×a=![]() a
a
∵△POA的面积是△POB面积的![]() 倍.
倍.
∴﹣a2+![]() a+1=
a+1=![]() ×
×![]() a,
a,
∴a=![]() 或a=﹣
或a=﹣![]() (舍)
(舍)
∴P(![]() ,1);
,1);
②如图1,
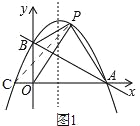
由(1)知,抛物线解析式为y=﹣x2+![]() x+1,
x+1,
∴抛物线的对称轴为x=![]() ,抛物线与x轴的另一交点为C(﹣
,抛物线与x轴的另一交点为C(﹣![]() ,0),
,0),
∵点A与点C关于对称轴对称,
∴QP+QA的最小值就是PC=![]() ;
;
(3)①当OB为平行四边形的边时,MN=OB=1,MN∥OB,
∵点N在直线AB上,
∴设M(m,﹣![]() m+1),
m+1),
∴N(m,﹣m2+![]() m+1),
m+1),
∴MN=|﹣m2+![]() m+1﹣(﹣
m+1﹣(﹣![]() m+1)|=|m2﹣2m|=1,
m+1)|=|m2﹣2m|=1,
Ⅰ、m2﹣2m=1,
解得,m=1±![]() ,
,
∴M(1+![]() ,
,![]() (1﹣
(1﹣![]() ))或M(1﹣
))或M(1﹣![]() ,
,![]() (1+
(1+![]() ))
))
Ⅱ、m2﹣2m=﹣1,
解得,m=1,
∴M(1,![]() );
);
②当OB为对角线时,OB与MN互相平分,交点为H,
∴OH=BH,MH=NH,
∵B(0,1),O(0,0),
∴H(0,![]() ),
),
设M(n,﹣![]() n+1),N(d,﹣d2+
n+1),N(d,﹣d2+![]() d+1)
d+1)
∴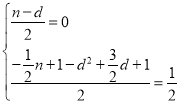 ,
,
∴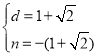 或
或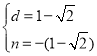 ,
,
∴M(﹣(1+![]() ),
),![]() (3+
(3+![]() ))或M(﹣(1﹣
))或M(﹣(1﹣![]() ),
),![]() (3﹣
(3﹣![]() ));
));
即:满足条件的点M的坐标(1+![]() ,
,![]() (1﹣
(1﹣![]() ))或(1﹣
))或(1﹣![]() ,﹣
,﹣![]() (1+
(1+![]() ))或(1,
))或(1,![]() )或M(﹣(1+
)或M(﹣(1+![]() ),
),![]() (3+
(3+![]() ))或M(﹣(1﹣
))或M(﹣(1﹣![]() ),
),![]() (3﹣
(3﹣![]() ));
));

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
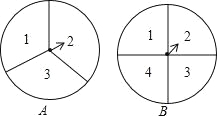
全能闯关100分系列答案【题目】某单位欲从内部招聘管理人员一名,对甲、乙、丙三名候选人进行了笔试和面试两项测试,三人的测试成绩如下表所示:
测试项目 | 测试成绩(分) | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,组织200名职工对三人利用投票推荐的方式进行民主评议,三人得票率(没有弃权票,每位职工只能推荐1人)如图所示,每得一票记作1分.
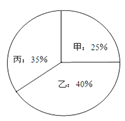
(1)请算出三人的民主评议得分.
(2)如果根据三项测试的平均成绩确定录用人选,那么谁将被录用(精确到0.01)?
(3)根据实际需要,单位将笔试、面试、民主评议三项测试得分按4︰3︰3![]() 的比例确定个人成绩,那么谁将被录用?
的比例确定个人成绩,那么谁将被录用?