题目内容
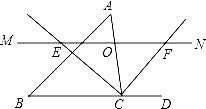
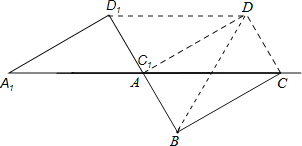
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②s=![]() (0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).
(0<x<2);③当x=1时,四边形ABC1D1是正方形;④当x=2时,△BDD1为等边三角形;其中正确的是 (填序号).
【答案】①②④
【解析】
试题分析:①根据矩形的性质,得∠DAC=∠ACB,再由平移的性质,可得出∠A1=∠ACB,A1D1=CB,从而证出结论;
②易得△AC1F∽△ACD,根据面积比等于相似比平方可得出s与x的函数关系式
③根据菱形的性质,四条边都相等,可推得当C1在AC中点时四边形ABC1D1是菱形.
④当x=2时,点C1与点A重合,可求得BD=DD1=BD1=2,从而可判断△BDD1为等边三角形.
解:①∵四边形ABCD为矩形,
∴BC=AD,BC∥AD
∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,
∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,
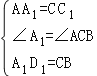 ,
,
∴△A1AD1≌△CC1B(SAS),
故①正确;
②易得△AC1F∽△ACD,
∴![]()
解得:S△AC1F=![]() (x﹣2)2 (0<x<2);故②正确;
(x﹣2)2 (0<x<2);故②正确;
③∵∠ACB=30°,
∴∠CAB=60°,
∵AB=1,
∴AC=2,
∵x=1,
∴AC1=1,
∴△AC1B是等边三角形,
∴AB=D1C1,
又AB∥BC1,
∴四边形ABC1D1是菱形,
故③错误;
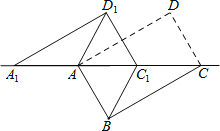
④如图所示:
则可得BD=DD1=BD1=2,
∴△BDD1为等边三角形,故④正确.
综上可得正确的是①②④.
故答案为:①②④

练习册系列答案
相关题目