题目内容

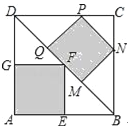
【题目】如图，在正方形ABCD中，点E，N，P，G分别在边AB，BC，CD，DA上，点M，F，Q都在对角线BD上，且四边形MNPQ和AEFG均为正方形，则的值等于 ．

【答案】

【解析】

试题根据辅助线的性质得到∠ABD=∠CBD=45°，四边形MNPQ和AEFG均为正方形，推出△BEF与△BMN是等腰直角三角形，于是得到FE=BE=AE=AB，BM=MN=QM，同理DQ=MQ，即可得到结论．

在正方形ABCD中， ∵∠ABD=∠CBD=45°， ∵四边形MNPQ和AEFG均为正方形，

∴∠BEF=∠AEF=90°，∠BMN=∠QMN=90°， ∴△BEF与△BMN是等腰直角三角形，

∴FE=BE=AE=AB，BM=MN=QM， 同理DQ=MQ，，

练习册系列答案
相关题目

【题目】如图，AB是⊙O的直径，CD切⊙O于点C，AD交⊙O于点E，AC平分∠BAD，连接BE．

（1）求证：CD⊥ED；

（2）若CD=4，AE=2，求⊙O的半径．

【题目】如图，在△ABC中，AB＝AC，AB是⊙O的直径，⊙O与BC交于点D，⊙O与AC交于点E，DF⊥AC于F，连接DE．

（1）求证：D为BC中点；

（2）求证：DF与⊙O相切；

（3）若⊙O的半径为5，tan∠C＝，则DE＝　 　．

【题目】如图，A（0，2），B（6，2），C（0，c）（c＞0），以A为圆心AB长为半径的交y轴正半轴于点D，与BC有交点时，交点为E，P为上一点．

（1）若c＝6+2，

①BC＝　 　，的长为　 　；

②当CP＝6时，判断CP与⊙A的位置关系，井加以证明；

（2）若c＝10，求点P与BC距离的最大值；

（3）分别直接写出当c＝1，c＝6，c＝9，c＝11时，点P与BC的最大距离（结果无需化简）

【题目】如图，一次函数y＝k1x＋b的图象与反比例函数y＝ (x＜0)的图象相交于点A(－1，2)、点B(－4，n)．

(1)求此一次函数和反比例函数的表达式；

(2)求△AOB的面积；

(3)在x轴上存在一点P，使△PAB的周长最小，求点P的坐标．

【题目】两栋居民楼之间的距离CD=30米，楼AC和BD均为10层，每层楼高3米．

（1）上午某时刻，太阳光线GB与水平面的夹角为30°，此刻B楼的影子落在A楼的第几层？

（2）当太阳光线与水平面的夹角为多少度时，B楼的影子刚好落在A楼的底部．

【题目】如图，边长为1的菱形ABCD中，∠DAB＝60度．连接对角线AC，以AC为边作第二个菱形ACC1D1，使∠D1AC＝60°；连接AC1，再以AC1为边作第三个菱形AC1C2D2，使∠D2AC1＝60°；…，按此规律所作的第n个菱形的边长为_____．

【题目】在如图的方格纸中（每个小方格的边长都是1个单位）有一点O和△ABC．

（1）请以点O为位似中心，把△ABC缩小为原来的一半（不改变方向），得到△A′B′C′；

（2）请用适当的方式描述△A′B′C′的顶点A′、B′、C′的位置．

【题目】受地震的影响，某超市鸡蛋供应紧张，需每天从外地调运鸡蛋1200斤．超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出800斤，乙养殖场每天最多可调出900斤，从两养殖场调运鸡蛋到超市的路程和运费如表：

到超市的路程(千米)

运费(元/斤千米)

甲养殖场

200

0.012

乙养殖场

140

0.015

(1)若某天调运鸡蛋的总运费为2670元，则从甲、乙两养殖场各调运了多少斤鸡蛋？

(2)设从甲养殖场调运鸡蛋x斤，总运费为W元，试写出W与x的函数关系式，怎样安排调运方案才能使每天的总运费最省？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网