题目内容
【题目】已知二次函数y=ax2+bx+c(a≠0).
(1)若b=1,a=﹣![]() c,求证:二次函数的图象与x轴一定有两个不同的交点;
c,求证:二次函数的图象与x轴一定有两个不同的交点;
(2)若a![]() 0,c=0,且对于任意的实数x,都有y
0,c=0,且对于任意的实数x,都有y![]() 1,求4a+b2的取值范围;
1,求4a+b2的取值范围;
(3)若函数图象上两点(0,y1)和(1,y2)满足y1y2>0,且2a+3b+6c=0,试确定二次函数图象对称轴与x轴交点横坐标的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据已知条件计算一元二次方程的判别式即可证得结论;
(2)根据已知条件求得抛物线的顶点纵坐标,再整理即可;
(3)将(0,y1)和(1,y2)分别代入函数解析式,由y1y2>0,及2a+3b+6c=0,得不等式组,变形即可得出答案.
解:(1)证明:∵y=ax2+bx+c(a≠0),
∴令y=0得:ax2+bx+c=0
∵b=1,a=﹣![]() c,
c,
∴△=b2﹣4ac=1﹣4(﹣![]() c)c=1+2c2,
c)c=1+2c2,
∵2c2≥0,
∴1+2c2>0,即△>0,
∴二次函数的图象与x轴一定有两个不同的交点;
(2)∵a<0,c=0,
∴抛物线的解析式为y=ax2+bx,其图象开口向下,
又∵对于任意的实数x,都有y≤1,
∴顶点纵坐标![]() ,
,
∴﹣b2≥4a,
∴4a+b2≤0;
(3)由2a+3b+6c=0,可得6c=﹣(2a+3b),
∵函数图象上两点(0,y1)和(1,y2)满足y1y2>0,
∴c(a+b+c)>0,
∴6c(6a+6b+6c)>0,
∴将6c=﹣(2a+3b)代入上式得,﹣(2a+3b)(4a+3b)>0,
∴(2a+3b)(4a+3b)<0,
∵a≠0,则9a2>0,
∴两边同除以9a2得,
![]() ,
,
∴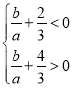 或
或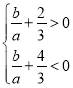 ,
,
∴![]() ,
,
∴二次函数图象对称轴与x轴交点横坐标的取值范围是:![]() .
.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目