题目内容
【题目】某农场拟建三件矩形饲养室,饲养室一面靠现有墙(墙可用长≤20m),中间用两道墙隔开,已知计划中的建筑材料可建围墙的总长为60m,设饲养室宽为x(m),总占地面积为y(m2)(如图所示). 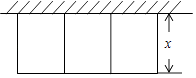
(1)求y关于x的函数表达式,并直接写出自变量x的取值范围;
(2)三间饲养室占地总面积有可能达到210m2吗?请说明理由.
【答案】
(1)解:设饲养室宽为x(m),则长为(60﹣4x)m,
∴y=x(60﹣4x)=﹣4x2+60x,
∵0<60﹣4x≤20,
∴10≤x<15
(2)解:不能,理由如下:
当y=210时,﹣4x2+60x=210,
解得:x= ![]() 或x=
或x= ![]() ,
,
∵x= ![]() <10,且x=
<10,且x= ![]() <10,
<10,
∴不能
【解析】(1)设饲养室宽为x(m),则长为(60﹣4x)m,根据长方形面积公式即可得,由墙可用长≤20m可得x的范围;(2)令y=210求出x,根据(1)中x的范围即可判断.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目