题目内容
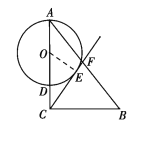
【题目】如图①,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点(不与
边上一点(不与![]() 重合),以
重合),以![]() 为直径作
为直径作![]() ,过
,过![]() 作
作![]() 切
切![]() 于
于![]() ,交
,交![]() 于
于![]() .
.
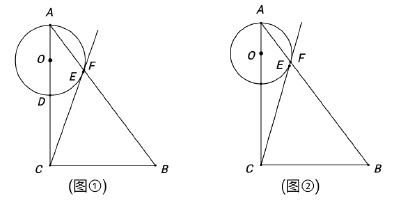
(1)若![]() 的半径为2,求线段
的半径为2,求线段![]() 的长;
的长;
(2)若![]() ,求
,求![]() 的半径;
的半径;
(3)如图②,若![]() ,点
,点![]() 关于
关于![]() 的对称点为点
的对称点为点![]() ,试求
,试求![]() 、
、![]() 两点之间的距离.
两点之间的距离.
【答案】(1)![]() ;(2)
;(2)![]() 的半径为3;(3)
的半径为3;(3)![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.
【解析】
(1)根据切线的性质得出∠OEC=90°,然后根据勾股定理即可求得;
(2)由勾股定理求得BC,然后通过证得△OEC∽△BCA,得到![]() =
=![]() ,即
,即![]() ,解得即可;
,解得即可;
(3)证得D和M重合,E和F重合后,通过证得△GBE∽△ABC,![]() ,即
,即![]() ,解得即可.
,解得即可.
(1)如图,连结![]() .
.
∵![]() 切
切![]() 于
于![]() ,
,
∴![]() .
.
∵![]() ,
,![]() 半径为2,
半径为2,
∴![]() ,
,![]() .
.
∴![]() ;
;
(2)设![]() 半径为
半径为![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 切
切![]() 于
于![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() ,
,
解得![]() .
.
∴![]() 的半径为3;
的半径为3;
(3)连结![]() 、
、![]() ,设
,设![]() 交
交![]() 于点
于点![]() ,
,
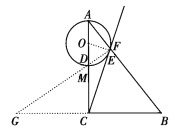
由对称性可知,![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() 切
切![]() 于
于![]() ,
,
∴![]() .
.
又![]() ,
,
∴![]() .又
.又![]() ,
,
∴![]() .
.
∴![]() .
.
∴点![]() 与点
与点![]() 重合.
重合.
∴![]() 、
、![]() 、
、![]() 三点在同一条直线上.
三点在同一条直线上.
连结![]() 、
、![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,即
,即![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() ,
,
∴![]() 、
、![]() 、
、![]() 三点在同一条直线上.
三点在同一条直线上.
∴![]() 、
、![]() 两点重合.
两点重合.
∵![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
∴![]() .
.
故![]() 、
、![]() 两点之间的距离为
两点之间的距离为![]() .
.

练习册系列答案
相关题目