题目内容
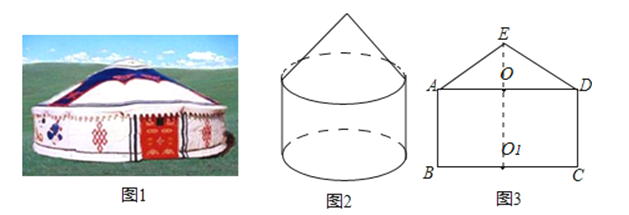
【题目】图(1)是一个蒙古包的照片,这个蒙古包可以近似看成是圆锥和圆柱组成的几何体,如图(2)所示.
(1)请画出这个几何体的俯视图;
(2)图(3)是这个几何体的正面示意图,已知蒙古包的顶部离地面的高度EO1=6米,圆柱部分的高OO1=4米,底面圆的直径BC=8米,求∠EAO的度数(结果精确到0.1°).
【答案】
(1)
画出俯视图,如图所示

(2)
解:连接EO1,如图所示:
∵EO1=6米,OO1=4米,
∴EO=EO1﹣OO1=6﹣4=2米,
∵AD=BC=8米,
∴OA=OD=4米,
在Rt△AOE中,tan∠EAO=![]() =
=![]() =
=![]() ,
,
则∠EAO≈26.6°.
【解析】(1)根据图2,画出俯视图即可;
(2)连接EO1 , 如图所示,由EO1﹣OO1求出EO的长,由BC=AD,O为AD中点,求出OA的长,在直角三角形AOE中,利用锐角三角函数定义求出tan∠EAO的值,即可确定出∠EAO的度数.
【考点精析】掌握圆锥的相关计算和圆柱的相关计算是解答本题的根本,需要知道圆锥侧面展开图是一个扇形,这个扇形的半径称为圆锥的母线;圆锥侧面积S=πrl;V圆锥=1/3πR2h.;圆柱的体积: V圆柱=πR2h.

练习册系列答案
相关题目