题目内容
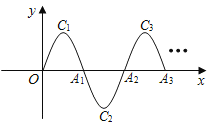
【题目】如图,一段抛物线:y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此变换进行下去,若点P(17,m)在这种连续变换的图象上,则m的值为( )
A.2B.﹣2C.﹣3D.3
【答案】D
【解析】
根据题意和题目中的函数解析式,可以得到点A1的坐标,从而可以求得OA1的长度,然后根据题意,即可得到点P(17,m)中m的值和x=1时对应的函数值相等,即可得答案.
∵y=﹣x(x﹣4)(0≤x≤4)记为C1,它与x轴交于两点O,A1,
∴点A1(4,0),
∴OA1=4,
∵OA1=A1A2=A2A3=A3A4……,
∴OA1=A1A2=A2A3=A3A4……=4,
∵点P(17,m)在这种连续变换的图象上,17÷4=4……1,
∴点P(17,m)在C5上,
∴x=17和x=1时的函数值相等,
∴m=﹣1×(1﹣4)=﹣1×(﹣3)=3,
故选D.

练习册系列答案
相关题目