题目内容
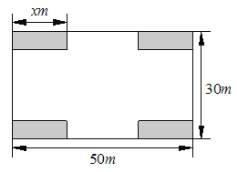
【题目】某小区业主委员会决定把一块长50![]() ,宽30
,宽30![]() 的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14
的矩形空地建成健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为全等的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14![]() ,不大于26
,不大于26![]() ,设绿化区较长边为
,设绿化区较长边为![]() ,活动区的面积为
,活动区的面积为![]() .
.
(1)直接写出:
①用![]() 的式子表示出口的宽度为_________;
的式子表示出口的宽度为_________;
②![]() 与
与![]() 的函数关系式及
的函数关系式及![]() 的取值范围__________________;
的取值范围__________________;
(2)若活动区造价为50元/![]() ,绿化区造价为40元/
,绿化区造价为40元/![]() ,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
,则绿化区边长怎么设计,健身广场投资费用最少,并求出最少费用.
【答案】(1)①50-2x;②y =-4x2+40x+1500(12≤x≤18)(2)69240元
【解析】
(1)①根据图形可得结论;
②根据题意可得y与x的关系式;
(2)根据列方程即可得到结论.
(1)①出口的宽度为:50-2x,
②绿化区的短边为:![]()
根据题意得,y=50×30-4x(x-10),
即y与x的函数关系式及x的取值范围为:y=-4x2+40x+1500(12≤x≤18);
故答案为:50-2x,y=-4x2+40x+1500(12≤x≤18);
(2)设费用为W,
由题意得,W=50(-4x2+40x+1500)+40×4x(x-10)=-40(x-5)2+76000,
∵a=-40<0,12≤x≤18
∴当x=18时,W最小,W最小值为69240元

练习册系列答案
相关题目