Question

【题目】已知抛物线y＝ax2+bx+c过点A（0，2），且抛物线上任意不同两点M（x1，y1），N（x2，y2）都满足；当x1＜x2＜0时（x1﹣x2）（y1﹣y2）＞0；当0＜x1＜x2时，（x1﹣x2）（y1﹣y2）＜0．以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B、C，且B在C的左侧，△ABC有一个内角为60°．则抛物线的解析式是__．

Answer 1

【答案】y＝﹣x2+2

【解析】

由A的坐标确定出c的值，根据已知不等式判断出y1﹣y2＜0，可得出抛物线的增减性，确定出抛物线对称轴为y轴，且开口向下，求出b的值，可得三角形ABC为等边三角形，确定出B的坐标，代入抛物线解析式即可．

解：∵抛物线过点A（0，2），

∴c＝2，

当x1＜x2＜0时，x1﹣x2＜0，由（x1﹣x2）（y1﹣y2）＞0，得到y1﹣y2＜0，

∴当x＜0时，y随x的增大而增大，

同理当x＞0时，y随x的增大而减小，

∴抛物线的对称轴为y轴，且开口向下，即b＝0，

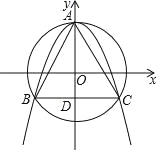
∵以O为圆心，OA为半径的圆与抛物线交于另两点B，C，如图所示，

∴△ABC为等腰三角形，

∵△ABC中有一个角为60°，

∴△ABC为等边三角形，且OC＝OA＝2，

设线段BC与y轴的交点为点D，则有BD＝CD，且∠OBD＝30°，

∴BD＝OBcos30°＝，OD＝OBsin30°＝1，

∵B在C的左侧，

∴B的坐标为（﹣，﹣1），

∵B点在抛物线上，且c＝2，b＝0，

∴3a+2＝﹣1，

解得：a＝﹣1，

则抛物线解析式为y＝﹣x2+2，

故答案为y＝﹣x2+2．