Question

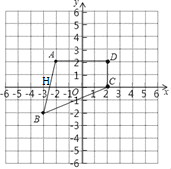
【题目】如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）（每个小正方形的边长均为1）．

（1）若点D与点A关于y轴对称则点D的坐标为　 　．

（2）将点B向右平移5个单位，再向上平移2个单位得到点C，则点C的坐标为　 　．

（3）请在图中表示出D、C两点，顺次连接ABCD，并求出A、B、C、D组成的四边形ABCD的面积．

Answer 1

【答案】（1）（2，2）；（2）（2，0）；（3）13

【解析】

（1）和（2）问利用直角坐标系中的平移变换即可找到相应点的坐标,（3）找到AB与x轴的交点H,求出H的坐标,利用四边形ABCD的面积为=S梯形ADCH+S△BHC即可进行求解.

解：（1）如图所示：D（2，2）；

故答案为：（2，2）；

（2）如图所示：C（2，0）；

故答案为：（2，0）；

（3）如图所示：设线段AB与x轴的交点为H,根据图像不难发现H为线段AB的中点,

∴H（-,0）

则四边形ABCD的面积为=S梯形ADCH+S△BHC==