��Ŀ����
����Ŀ�����Ķ����в��ϣ�
���⣺��ͼ����������![]() ��ƽ���ı���
��ƽ���ı���![]() �У���
����![]() ��
��![]() ��
��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ���߶�
���߶�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��
��
̽������![]() ��
��![]() �ļн�Ϊ���ٶ�ʱ��ƽ���ı���
�ļн�Ϊ���ٶ�ʱ��ƽ���ı���![]() �������Σ�
��������
С��ͬѧ��˼·�ǣ����ȿ���˵���ı���![]() �Ǿ��Σ�Ȼ���ӳ�
�Ǿ��Σ�Ȼ���ӳ�![]() ��
��![]() �ڵ�
�ڵ�![]() ������ȫ�������Σ�������������̽��������Ĵ𰸣�
������ȫ�������Σ�������������̽��������Ĵ𰸣�
����ο�С��ͬѧ��˼·��̽�������������⣮
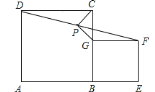
��1����֤���ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
��2��![]() ��
��![]() �ļн�Ϊ________��ʱ���ı���
�ļн�Ϊ________��ʱ���ı���![]() �������Σ�
��������
���ɣ�
���𰸡�(1)�����������2��90.
��������
��1����������ABCD���á�EBG��90����������һ������ֱ�ǵ�ƽ���ı����Ǿ��Σ�����֤���ı���BEFG�Ǿ��Σ�
��2�������������ߣ��ӳ�GP��DC�ڵ�H��������������ƽ���ı��ε����ʣ�����AAS����DHP�ա�FGP������HP��GP������CPG��90��ʱ������SAS��֤��CPH�ա�CPG������ȫ���������������ε����ʣ����ɵ�BG��GF��������һ���ڱ���ȵ�ƽ���ı��������Σ��ɵ�BEFG�����Σ�����EBG��90���������ı���BEFG�������Σ�
��1����������ABCD�У���ABC��90�㣬
���EBG��90�㣬
��BEFG�Ǿ�����
��2��90�㣻
���ɣ��ӳ�GP��DC�ڵ�H��
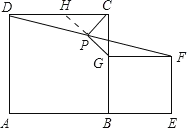
��������ABCD��ƽ���ı���BEFG�У�AB��DC��BE��GF��
��DC��GF��
���HDP����GFP����DHP����FGP��
��P���߶�DF���е㣬
��DP��FP��
���DHP�ա�FGP��
��HP��GP��
����CPG��90��ʱ����CPH����CPG��
��CP��CP��
���CPH�ա�CPG��
��CH��CG��
��������ABCD��DC��BC��
��DH��BG��
�ߡ�DHP�ա�FGP��
��DH��GF��
��BG��GF��
��BEFG������
�ɣ�1��֪�ı���BEFG�Ǿ��Σ�
���ı���BEFG�������Σ�






