题目内容
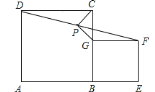
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

【答案】![]() 或
或![]()
【解析】
当点P在AF上时,由翻折的性质可求得PF=FC=4,然后再求得正方形的对角线AF的长,从而可得到PA的长;当点P在BE上时,由正方形的性质可知BP为AF的垂直平分线,则AP=PF,由翻折的性质可求得PF=FC=4,故此可得到AP的值.
如图1所示:
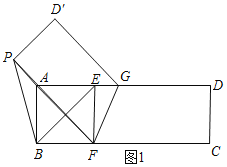
由翻折的性质可知PF=CF=4,
∵ABFE为正方形,边长为2,
∴AF=2![]() .
.
∴PA=4-2![]() .
.
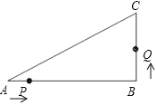
如图2所示:

由翻折的性质可知PF=FC=4.
∵ABFE为正方形,
∴BE为AF的垂直平分线.
∴AP=PF=4.
故答案为:4或4-2![]() .
.

练习册系列答案
相关题目