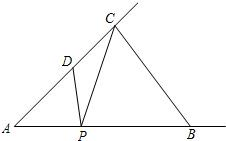
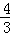题目内容
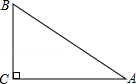
已知在△ABC中,∠A=45°,AB=7,tanB=
,动点P、D分别在射线AB、AC上,且∠DPA=∠ACB,设AP=x,△PCD的面积为y.
(1)求△ABC的面积;
(2)如图,当动点P、D分别在边AB、AC上时,求y关于x的函数解析式,并写出函数的定义域;
(3)如果△PCD是以PD为腰的等腰三角形,求线段AP的长.
| 4 |
| 3 |
(1)求△ABC的面积;
(2)如图,当动点P、D分别在边AB、AC上时,求y关于x的函数解析式,并写出函数的定义域;
(3)如果△PCD是以PD为腰的等腰三角形,求线段AP的长.

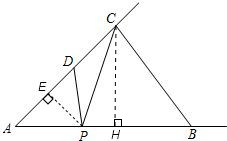
(1)作CH⊥AB,垂足为点H,设CH=m;
∵tanB=
,∴BH=
m(1分)
∵∠A=45°,∴AH=CH=m
∴m+
m=7;(1分)
∴m=4;(1分)
∴△ABC的面积等于
×7×4=14;(1分)
(2)∵AH=CH=4,
∴AC=4
∵∠DPA=∠ACB,∠A=∠A,
∴△ADP∽△ABC;(1分)
∴
=
,即
=
∴CD=
;(1分)
作PE⊥AC,垂足为点E;
∵∠A=45°,AP=x,
∴PE=
;(1分)
∴所求的函数解析式为y=
•
•
,即y=-
x2+2x;(1分)
当D到C时,AP最大.
∵△CPA∽△BCA
∴
=
∴AP=
=
,
∴定义域为0<x<
;(1分)
(3)由△ADP∽△ABC,得
=
,即
=
;
∴PD=
;(1分)
∵△PCD是以PD为腰的等腰三角形,
∴有PD=CD或PD=PC;
(i)当点D在边AC上时,
∵∠PDC是钝角,只有PD=CD
∴
=
;
解得x=
;(1分)
(ii)当点D在边AC的延长线上时,CD=
,PC=
(1分)
如果PD=CD,那么
=
解得x=16(1分)
如果PD=PC,那么
=
解得x1=32,x2=
(不符合题意,舍去)(1分)
综上所述,AP的长为
,或16,或32.
∵tanB=
| 4 |
| 3 |
| 3 |
| 4 |
∵∠A=45°,∴AH=CH=m
∴m+
| 3 |
| 4 |
∴m=4;(1分)
∴△ABC的面积等于
| 1 |
| 2 |
(2)∵AH=CH=4,
∴AC=4
| 2 |
∵∠DPA=∠ACB,∠A=∠A,
∴△ADP∽△ABC;(1分)
∴
| AD |
| AB |
| AP |
| AC |
4
| ||
| 7 |
| x | ||
4
|
∴CD=
| 32-7x | ||
4
|
作PE⊥AC,垂足为点E;
∵∠A=45°,AP=x,
∴PE=
| x | ||
|
∴所求的函数解析式为y=
| 1 |
| 2 |
| 32-7x | ||
4
|
| x | ||
|
| 7 |
| 16 |
当D到C时,AP最大.
∵△CPA∽△BCA
∴
| AP |
| AC |
| AC |
| AB |
∴AP=
| AC2 |
| AB |
| 32 |
| 7 |
∴定义域为0<x<
| 32 |
| 7 |
(3)由△ADP∽△ABC,得
| PD |
| BC |
| AP |
| AC |
| PD |
| 5 |
| x | ||
4
|
∴PD=
| 5x | ||
4
|
∵△PCD是以PD为腰的等腰三角形,
∴有PD=CD或PD=PC;
(i)当点D在边AC上时,
∵∠PDC是钝角,只有PD=CD
∴
| 5x | ||
4
|
| 32-7x | ||
4
|
解得x=
| 8 |
| 3 |
(ii)当点D在边AC的延长线上时,CD=
| 7x-32 | ||
4
|
| (x-4)2+42 |
如果PD=CD,那么
| 32-7x | ||
4
|
| (x-4)2+42 |
解得x=16(1分)
如果PD=PC,那么
| 5x | ||
4
|
| (x-4)2+42 |
解得x1=32,x2=
| 32 |
| 7 |
综上所述,AP的长为
| 8 |
| 3 |


练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目