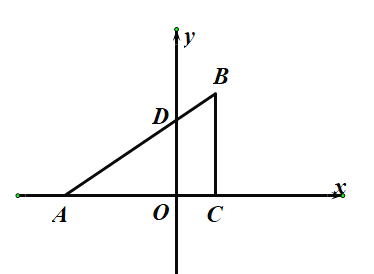题目内容
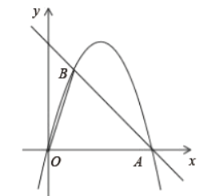
【题目】如图,抛物线y = x2+bx+c过点A (-1,2),且关于y轴对称,点C与点B(a,0)(a>1)关于原点对称,直线AC交抛物线于点D.
(1)求此抛物线的解析式;
(2)连接OA,BD,当OA//BD时,求a的值;
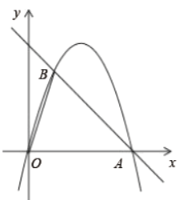
(3)若直线AC交抛物线![]() 于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.
于E,F两点(点E在点F的左侧),且EA=DF,求直线AC的解析式.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)y=2x+4.
;(3)y=2x+4.
【解析】
(1)根据抛物线的对称轴可得b的值,代入A点的坐标即可求出c的值;
(2)根据OA//BD和A点坐标可求出D点坐标,然后代入函数解析式即可解答;
(3)设A(xA,yA),D(xD,yD),E(xE,yE),F(xF,yF),根据EA=DF可得,xA-xE=xF-xD,xA+xD=xF+xE,根据A(-1,2),C(-a,0)求出直线AC解析式为![]() ,然后与两个抛物线联立可得关于a的方程,解出a的值然后即可求出直线AC的解析式.
,然后与两个抛物线联立可得关于a的方程,解出a的值然后即可求出直线AC的解析式.
(1)∵抛物线关于y轴对称,
∴b=0,
把A (-1,2),b=0代入y = x2+bx+c,得c=1,
∴抛物线解析式为:![]() ;
;
(2)∵B、C关于原点对称,B(a,0)
∴C(-a,0),
∵OA∥BD,
∴点A是CD中点,
∵A (-1,2),
∴D (a-2,4),
把D (a-2,4)代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
∵a>1,
∴![]() ;
;
(3)设A(xA,yA),D(xD,yD),E(xE,yE),F(xF,yF),
∵EA=DF,∴xA-xE=xF-xD ∴xA+xD=xF+xE,
把A(-1,2),C(-a,0)代入求得直线AC解析式为:![]() ,
,
联立,得: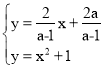 ,
,
∴![]() ,
,
∴xA+xD=![]() ,
,
联立,得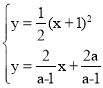 ,
,
∴![]() ,
,
∴xF+xE=![]() ,
,
∴![]() =
=![]() ,
,
解得:a=2,经检验a=2是原方程的解且符合题意,
∴直线AC解析式为:y=![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】某班级从甲、乙两位同学中选派一人参加知识竞赛,老师对他们的五次模拟成绩(单位:分)进行了整理,并计算出甲成绩的平均数是80分,甲、乙成绩的方差分别是320,40,但绘制的统计图表尚不完整.
甲、乙两人模拟成绩统计表
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
甲成绩 | 90 | 100 | 90 | 50 |
|
乙成绩 | 80 | 70 | 80 | 90 | 80 |
甲、乙两人模拟成绩折线图
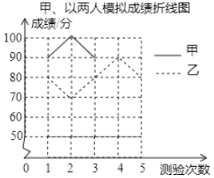
根据以上信息,请你解答下列问题:
(1)![]()
(2)请完成图中表示甲成绩变化情况的折线;
(3)求乙成绩的平均数;
(4)从平均数和方差的角度分析,谁将被选中.